题目内容
对于实数a,将满足“0≤y<1且x-y为整数”的实数y称为实数x的小数部分,用记号||x||表示,对于实数a,无穷数列{an}满足如下条件:a1=|a,an+1=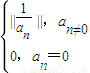 其中n=1,2,3,…
其中n=1,2,3,…(1)若a=
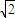 ,求数列{an};
,求数列{an};(2)当a
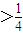 时,对任意的n∈N*,都有an=a,求符合要求的实数a构成的集合A.
时,对任意的n∈N*,都有an=a,求符合要求的实数a构成的集合A.(3)若a是有理数,设a=
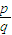 (p 是整数,q是正整数,p、q互质),问对于大于q的任意正整数n,是否都有an=0成立,并证明你的结论.
(p 是整数,q是正整数,p、q互质),问对于大于q的任意正整数n,是否都有an=0成立,并证明你的结论.
【答案】分析:(1)由题设知 =
= ,a2=
,a2= =
=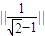 =
= =
= ,由此能求出
,由此能求出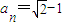 .
.
(2)由a1=||a||=a,知 ,1<
,1< <4,由此进行分类讨论,能求出符合要求的实数a构成的集合A.
<4,由此进行分类讨论,能求出符合要求的实数a构成的集合A.
(3)成立.证明:由a是有理数,可知对一切正整数n,an为0或正有理数,可设 ,由此利用分类讨论思想能够推导出数列{am}中am以及它之后的项均为0,所以对不大q的自然数n,都有an=0.
,由此利用分类讨论思想能够推导出数列{am}中am以及它之后的项均为0,所以对不大q的自然数n,都有an=0.
解答:解:(1)∵满足“0≤y<1且x-y为整数”的实数y称为实数x的小数部分,用记号||x||表示,
a1=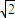 ,an+1=
,an+1= 其中n=1,2,3,…
其中n=1,2,3,…
∴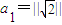 =
=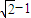 ,a2=
,a2=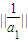 =
= =
= =
= ,…(2分)
,…(2分)
ak=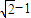 ,则ak+1=
,则ak+1= =
= =
= ,
,
所以 .…(4分)
.…(4分)
(2)∵a1=||a||=a,∴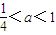 ,∴1<
,∴1< <4,
<4,
①当 ,即1<
,即1<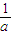 <2时,
<2时, =
= =
=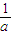 -1=a,
-1=a,
所以a2+a-1=0,
解得a= ,(a=
,(a= ∉(
∉( ,1),舍去).…(6分)
,1),舍去).…(6分)
②当 ,即2≤
,即2≤ <3时,a2=
<3时,a2= =
=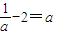 ,
,
所以a2+2a-1=0,
解得a= =
= ,(a=-
,(a=- ∉(
∉( ,
, ],舍去).…(7分)
],舍去).…(7分)
③当 ,即3
,即3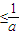 <4时,
<4时, ,
,
所以a2+3a-1=0,
解得a= (a=
(a= ,舍去).…(9分)
,舍去).…(9分)
综上,{a= ,a=
,a= ,a=
,a= }.…(10分)
}.…(10分)
(3)成立.…(11分)
证明:由a是有理数,可知对一切正整数n,an为0或正有理数,
可设 (pn是非负整数,qn是正整数,且
(pn是非负整数,qn是正整数,且 既约).…(12分)
既约).…(12分)
①由 ,得0≤p1≤q;…(13分)
,得0≤p1≤q;…(13分)
②若pn≠0,设qn=apn+β(0≤βPn,α,β是非负整数)
则 =a+
=a+ ,而由
,而由 ,得
,得 =
=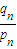 ,
,
 =
= =
= ,
,
故Pn+1=β,qn+1=Pn,得0≤Pn+1<Pn.…(14分)
若Pn=0,则pn+1=0,…(15分)
若a1,a2,a3,…,aq均不为0,则这q正整数互不相同且都小于q,
但小于q的正整数共有q-1个,矛盾.…(17分)
故a1,a2,a3,…,aq中至少有一个为0,即存在m(1≤m≤q),使得am=0.
从而数列{am}中am以及它之后的项均为0,所以对不大q的自然数n,都有an=0.…(18分)
(其它解法可参考给分)
点评:本题考查数列的通项公式的求法,考查集合的求法,考查an=0是否成立的判断与证明.综合性强,计算量大,难度较高,对数学思维能力的要求较高.解题时要认真审题,注意等价转化思想和分类讨论思想的合理运用.
 =
= ,a2=
,a2= =
=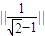 =
= =
= ,由此能求出
,由此能求出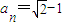 .
.(2)由a1=||a||=a,知
 ,1<
,1< <4,由此进行分类讨论,能求出符合要求的实数a构成的集合A.
<4,由此进行分类讨论,能求出符合要求的实数a构成的集合A.(3)成立.证明:由a是有理数,可知对一切正整数n,an为0或正有理数,可设
 ,由此利用分类讨论思想能够推导出数列{am}中am以及它之后的项均为0,所以对不大q的自然数n,都有an=0.
,由此利用分类讨论思想能够推导出数列{am}中am以及它之后的项均为0,所以对不大q的自然数n,都有an=0.解答:解:(1)∵满足“0≤y<1且x-y为整数”的实数y称为实数x的小数部分,用记号||x||表示,
a1=
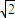 ,an+1=
,an+1= 其中n=1,2,3,…
其中n=1,2,3,…∴
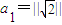 =
=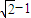 ,a2=
,a2=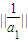 =
= =
= =
= ,…(2分)
,…(2分)ak=
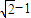 ,则ak+1=
,则ak+1= =
= =
= ,
,所以
 .…(4分)
.…(4分)(2)∵a1=||a||=a,∴
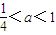 ,∴1<
,∴1< <4,
<4,①当
 ,即1<
,即1<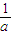 <2时,
<2时, =
= =
=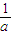 -1=a,
-1=a,所以a2+a-1=0,
解得a=
 ,(a=
,(a= ∉(
∉( ,1),舍去).…(6分)
,1),舍去).…(6分)②当
 ,即2≤
,即2≤ <3时,a2=
<3时,a2= =
=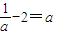 ,
,所以a2+2a-1=0,
解得a=
 =
= ,(a=-
,(a=- ∉(
∉( ,
, ],舍去).…(7分)
],舍去).…(7分)③当
 ,即3
,即3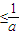 <4时,
<4时, ,
,所以a2+3a-1=0,
解得a=
 (a=
(a= ,舍去).…(9分)
,舍去).…(9分)综上,{a=
 ,a=
,a= ,a=
,a= }.…(10分)
}.…(10分)(3)成立.…(11分)
证明:由a是有理数,可知对一切正整数n,an为0或正有理数,
可设
 (pn是非负整数,qn是正整数,且
(pn是非负整数,qn是正整数,且 既约).…(12分)
既约).…(12分)①由
 ,得0≤p1≤q;…(13分)
,得0≤p1≤q;…(13分)②若pn≠0,设qn=apn+β(0≤βPn,α,β是非负整数)
则
 =a+
=a+ ,而由
,而由 ,得
,得 =
=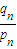 ,
, =
= =
= ,
,故Pn+1=β,qn+1=Pn,得0≤Pn+1<Pn.…(14分)
若Pn=0,则pn+1=0,…(15分)
若a1,a2,a3,…,aq均不为0,则这q正整数互不相同且都小于q,
但小于q的正整数共有q-1个,矛盾.…(17分)
故a1,a2,a3,…,aq中至少有一个为0,即存在m(1≤m≤q),使得am=0.
从而数列{am}中am以及它之后的项均为0,所以对不大q的自然数n,都有an=0.…(18分)
(其它解法可参考给分)
点评:本题考查数列的通项公式的求法,考查集合的求法,考查an=0是否成立的判断与证明.综合性强,计算量大,难度较高,对数学思维能力的要求较高.解题时要认真审题,注意等价转化思想和分类讨论思想的合理运用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目