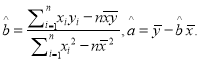题目内容
【题目】在公差不为零的等差数列
中，已知
，且
成等比数列．
（1）求数列的通项公式；
（2）设数列的前
项和为
，记
，求数列
的前
项和
．
【答案】（1）
（2）
【解析】
试题分析：（1）求等差数列通项公式，基本方法为待定系数法，即根据条件列两个关于首项与公差的方程：
，注意公差不为零，解得
，代入通项公式得
（2）先根据等差数列求和公式得
，因此代入化简数列
通项公式
，所以利用裂项相消法求和，即
，
试题解析：①设
的公差为
，依题意得
，．．．．．．．．．．．．．．．．．3分
解得，．．．．．．．．．．．．．．．．．．．．．．．．5分
∴．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分
②，
，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．9分
，故．．．．．．12分
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
