题目内容
(本小题满分14分)若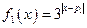 ,
,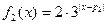 ,
, ,
,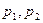 为常
为常
数,且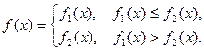
(Ⅰ)求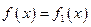 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用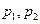 表示);
表示);
(Ⅱ)设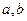 为两实数,
为两实数,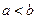 且
且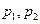
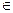
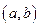 ,若
,若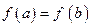
求证: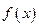 在区间
在区间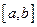 上的单调增区间的长度和为
上的单调增区间的长度和为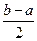 (闭区间
(闭区间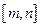 的长度定义为
的长度定义为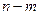 ).
).
解:(Ⅰ)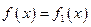 恒成立
恒成立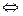

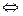

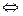
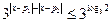 ;
;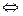
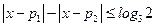 (*)
(*)
因为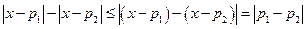 ,
,
所以,故只需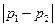
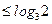 (*)恒成立.
(*)恒成立.
综上所述,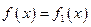 对所有实数成立的充要条件是
对所有实数成立的充要条件是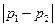
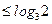 . ………4分
. ………4分
(Ⅱ)1°如果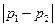
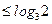 ,则的图象关于直线
,则的图象关于直线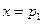 对称.因为
对称.因为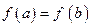 ,所以区间
,所以区间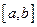 关于直线
关于直线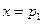 对称.
对称.
因为减区间为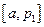 ,增区间为
,增区间为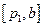 ,所以单调增区间的长度和为
,所以单调增区间的长度和为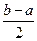 . ………6分
. ………6分
2°如果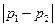
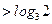 .
.
(1)当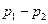
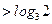 时.
时.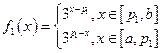 ,
,
当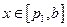 ,
,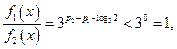 因为
因为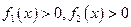 ,所以
,所以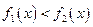 ,故
,故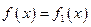 =
=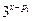 .
.
当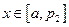 ,
,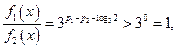 因为
因为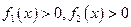 ,所以
,所以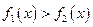 ,故
,故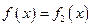 =
=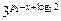 .
.
因为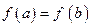 ,所以
,所以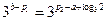 ,所以
,所以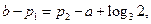 即
即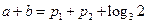 .
.
当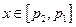 时,令
时,令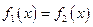 ,则
,则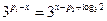 ,所以
,所以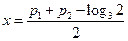 ,
,
当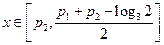 时,
时,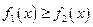 ,所以
,所以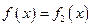 =
=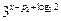 ;
;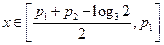 时,
时, ,所以
,所以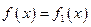 =
=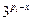 .
.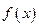 在区间
在区间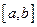 上的单调增区间的长度和
上的单调增区间的长度和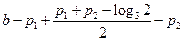
=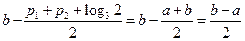 . …………10分
. …………10分
(2)当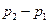
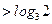 时.
时.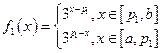 ,
,
当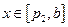 ,
,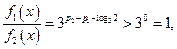 因为
因为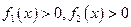 ,所以
,所以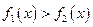 ,故
,故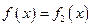 解析
解析

练习册系列答案
相关题目
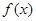 的定义域是
的定义域是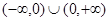 ,且
,且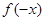 =
=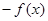 .已知当x>0时
.已知当x>0时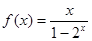
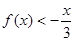 .
.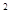 +4x+3,g(x)为一次函数,若f(g(x))=x
+4x+3,g(x)为一次函数,若f(g(x))=x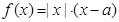 .
. 的奇偶性;
的奇偶性;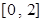 上的最小值为
上的最小值为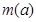 ,求
,求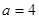 ,证明:方程
,证明:方程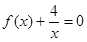 有两个不同的正数解.
有两个不同的正数解. 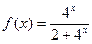 ,
, 是R上的增函数;(6分)
是R上的增函数;(6分)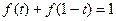 ;(4分)
;(4分)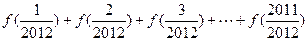 。(4分)
。(4分)
 的定义域
的定义域 满足
满足 ,且
,且 有唯
有唯 的表达式 ;
的表达式 ; ,且
,且 =
= ,求数列
,求数列 的通项公式。
的通项公式。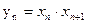 ,数列{
,数列{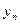 }的前
}的前  项和为
项和为  ,是否存在k∈N*,使得
,是否存在k∈N*,使得
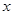 ,设
,设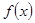 取
取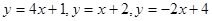 三个函数中的最小值,用分段函数写出
三个函数中的最小值,用分段函数写出 的定义域为
的定义域为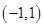 ,且同时满足下列条件:
,且同时满足下列条件: 求
求 的取值范围。
的取值范围。