题目内容
已知函数 满足
满足 ,且
,且 有唯
有唯
一实数解。
(1)求 的表达式 ;
的表达式 ;
(2)记 ,且
,且 =
= ,求数列
,求数列 的通项公式。
的通项公式。
(3)记 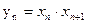 ,数列{
,数列{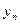 }的前
}的前  项和为
项和为  ,是否存在k∈N*,使得
,是否存在k∈N*,使得
对任意n∈N*恒成立?若存在,求出k的最小值,若不存在,请说明理由.
解:(1) 由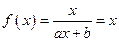 即
即 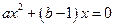 有唯一解,
有唯一解,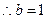
又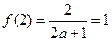
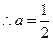 ,
, 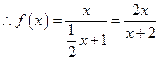
(2) 由 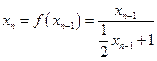
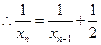 又
又 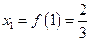
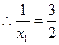 , 数列
, 数列 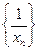 是以首项为
是以首项为 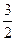 ,公差为
,公差为  的等差数列
的等差数列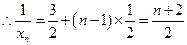
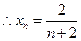
(3) 由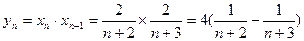
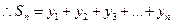 =
=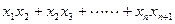
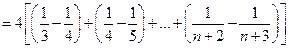
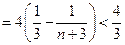
要使 对任意n∈N*恒成立, 只需
对任意n∈N*恒成立, 只需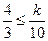 即
即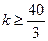
又k∈N* ∴k的最小值为14.
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2)利用单调性的定义证明函数f(x)在区间[1,+∞
(2)利用单调性的定义证明函数f(x)在区间[1,+∞ 上是增函数.
上是增函数.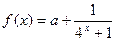 是奇函数.
是奇函数. a的值,并指出函数
a的值,并指出函数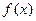 的单调性(不必说明单调性理
的单调性(不必说明单调性理 由);
由);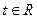 ,不等式
,不等式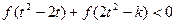 恒成立,求
恒成立,求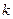 的取值范围.
的取值范围. 是定义在
是定义在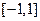 上的函数,且对任意
上的函数,且对任意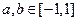 ,当
,当 时,都有
时,都有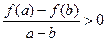 ;
;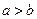 时,比较
时,比较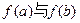 的大小;
的大小;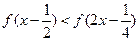 ;
;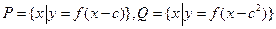 且
且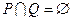 ,求
,求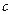 的取值范围。
的取值范围。 .
. 的反函数
的反函数 ;
; .
.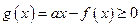 对任意
对任意 恒成立
恒成立 ,求实数
,求实数 的取值范围;
的取值范围;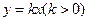 有且仅有三个公共点,且公共点的横坐标的最大值为
有且仅有三个公共点,且公共点的横坐标的最大值为 ,求证:
,求证: .
. 为奇函数且
为奇函数且
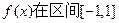 上是增函数。
上是增函数。 恒成立,求t的最小值。
恒成立,求t的最小值。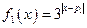 ,
,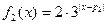 ,
, ,
,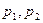 为常
为常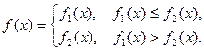
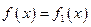 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用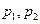 表示);
表示);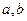 为两实数,
为两实数,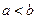 且
且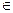
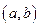 ,若
,若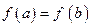
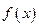 在区间
在区间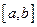 上的单调增区间的长度和为
上的单调增区间的长度和为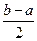 (闭区间
(闭区间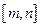 的长度定义为
的长度定义为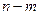 ).
). |x|在x∈[-1,1]的图象上有两点A、B,
|x|在x∈[-1,1]的图象上有两点A、B, AB∥
AB∥