Question

2．经过三棱锥A-BCD的棱DA、CD的中点E、F和面ABC重心G的平面，与三棱锥的各面的交线形成的几何图形是（　　）

• A． 三角形
• B． 梯形
• C． 菱形
• D． 平面四边形

Answer 1

分析 由题意画出图形，在平面ABC中，过G作MN∥AC，交AB于M，交BC于N．连接EM、FN，则四边形EMNF为所求平面图形．由EF∥MN且MN=$\frac{2}{3}AC＞\frac{1}{2}AC=EF$得四边形EMNF为梯形．

解答 解：如图，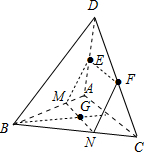

在平面ABC中，过G作MN∥AC，交AB于M，交BC于N．
∴MN∥EF，连接EM、FN，则四边形EMNF为所求平面图形．
∵EF∥MN，又MN=$\frac{2}{3}AC＞\frac{1}{2}AC=EF$，
∴四边形EMNF为梯形．
故选：B．

点评 本题考查棱锥的结构特征，考查了学生的空间想象能力和思维能力，考查了梯形的判定，是中档题．