题目内容
(1)已知等差数列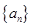 ,
,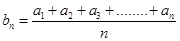 (
(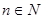 ),求证:
),求证: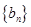 仍为等差数列;
仍为等差数列;
(2)已知等比数列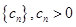
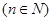 ),类比上述性质,写出一个真命题并加以证明.
),类比上述性质,写出一个真命题并加以证明.
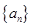 ,
,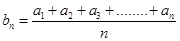 (
(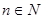 ),求证:
),求证: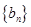 仍为等差数列;
仍为等差数列;(2)已知等比数列
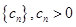
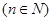 ),类比上述性质,写出一个真命题并加以证明.
),类比上述性质,写出一个真命题并加以证明.(1)等差数列的定义运用,根据相邻两项的差为定值,来证明。
(2)若
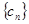 为等比数列,
为等比数列,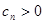 (
(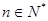 ),
),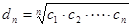 ,则
,则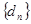 为等比数列
为等比数列试题分析:证明:(1)
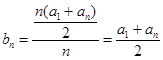 , 2分
, 2分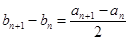 , 4分
, 4分 为等差数列
为等差数列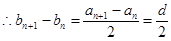 为常数, 6分
为常数, 6分所以
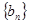 仍为等差数列; 7分
仍为等差数列; 7分(2)类比命题:若
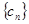 为等比数列,
为等比数列,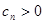 (
(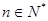 ),
),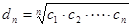 ,则
,则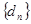 为等比数列
为等比数列9分
证明:
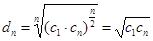 , 11分,为常数, 13分
, 11分,为常数, 13分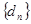 为等比数列 14分
为等比数列 14分点评:考查了类比推理的运用,以及等差数列的定义,属于基础题。

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
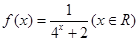 .
.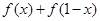 的值;
的值;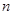 项和公式的推导方法,求:
项和公式的推导方法,求: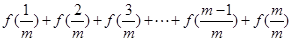 的值.
的值. 中,
中, ;设数列
;设数列 的前
的前 项和为
项和为 ,则
,则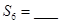
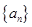 的前
的前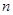 项和为
项和为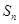 ,
,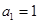 ,
,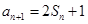
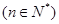 ,等差数列
,等差数列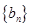 满足
满足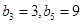 .
.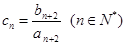 ,求证
,求证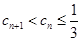 .
. 中,
中, (
( ),则
),则 .
.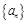 是等差数列,
是等差数列,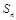 是其前
是其前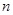 项的和,且
项的和,且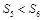 ,
,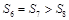 ,则下列结论错误的是
,则下列结论错误的是


 和
和 均为
均为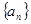 的通项公式为
的通项公式为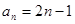 ,数列
,数列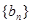 的前n项和为
的前n项和为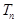 ,且满足
,且满足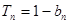
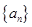 中是否存在使得
中是否存在使得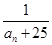 是
是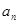 }中,
}中,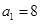 ,
,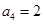 ,且满足
,且满足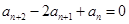
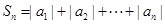 ,求
,求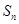 .
.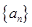 是等差数列,其中
是等差数列,其中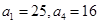 ]
]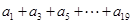 值。]
值。]