题目内容
3．设全集为R，函数f（x）=$\sqrt{{{log}_2}x-1}$的定义域为M，则∁RM=（ ）| A． | （-∞，1） | B． | [2，+∞） | C． | （-∞，2） | D． | （0，2） |
分析 根据函数成立的条件即可求函数的定义域．结合集合的基本运算进行求解即可．
解答 解：要使函数有意义，则log2x-1≥0，
即log2x≥1，则x≥2，即M=[2，+∞），
则∁RM=（-∞，2），
故选：C．
点评 本题主要考查集合的基本运算，结合函数定义域的求解，求出函数的定义域是解决本题的关键．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
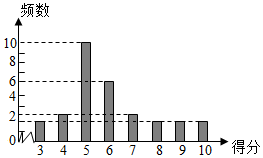为了普及环保知识，增强环保意识，随机抽取某大学30民学生参加环保知识测试，得分（10分制）如图所示，假设得分的中位数为me，众数为mσ，平均数为$\overline{x}$，则me，mσ，$\overline{x}$之间的大小关系是mσ＜me＜$\overline{x}$．
8．下列说法正确的是（ ）
| A． | “x2+x-2＞0”是“x＞l”的充分不必要条件 | |
| B． | “若am2＜bm2，则a＜b的逆否命题为真命题 | |
| C． | 命题“?x∈R，使得2x2-1＜0”的否定是：“?x∈R，均有2x2-1＜0” | |
| D． | 命题“若x=$\frac{π}{4}$，则tanx=1的逆命题为真命题 |