题目内容
6.设数列{an}的前n项和Sn满足Sn=2an-a1,且a3,a2+1,a1成等差数列.若log2an+1≤71,则n的最大值等于( )| A. | 67 | B. | 68 | C. | 69 | D. | 70 |
分析 Sn=2an-a1,令n=1,可得:a1=2a1-a1;令n=2,可得a2=2a1;令n=3,可得:a3=2a2=4a1.由于a3,a2+1,a1成等差数列.可得2(a2+1)=a3+a1,代入解得a1=2.当n≥2时,an=Sn-Sn-1,化为an=2an-1.再利用等比数列的通项公式、对数的运算性质即可得出.
解答 解:∵Sn=2an-a1,令n=1,可得:a1=2a1-a1;令n=2,则a1+a2=2a2-a1,可得a2=2a1;令n=3,可得:a3=2a2=4a1.
∵a3,a2+1,a1成等差数列.∴2(a2+1)=a3+a1,代入可得:2(2a1+1)=5a1,解得a1=2.
当n≥2时,an=Sn-Sn-1=2an-a1-(2an-1-a1),化为an=2an-1.
∴数列{an}是等比数列,首项为2,公比为2.
∴an=2n.
∵log2an+1≤71,
∴n+1≤71,解得n≤70.
则n的最大值等于70.
故选:D.
点评 本题考查了递推关系、等比数列的通项公式、对数的运算性质、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16.已知函数f(x)=sin(2x-$\frac{π}{2}$),下列结论错误的是( )
| A. | f(x)的最小正周期为π | B. | f(x)在区间$[{0,\frac{π}{2}}]$上是增函数 | ||
| C. | f(x)的图象关于点$({-\frac{3π}{4},0})$对称 | D. | f(x)的图象关于直线$x=\frac{5π}{4}$对称 |
1.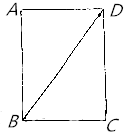 如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
 如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )| A. | $\frac{1}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{8}{25}$ | D. | $\frac{1}{3}$ |
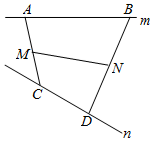 如图,已知m,n是异面直线,点A,B∈m,且AB=6,点C,D∈n,且CD=4,若M,N分别是AC,BD的中点,MN=2$\sqrt{2}$,则m与n所成角的余弦值是$\frac{5}{12}$.
如图,已知m,n是异面直线,点A,B∈m,且AB=6,点C,D∈n,且CD=4,若M,N分别是AC,BD的中点,MN=2$\sqrt{2}$,则m与n所成角的余弦值是$\frac{5}{12}$.