Question

【题目】在平面直角坐标系 中，以坐标原点为极点， 轴正半轴为极轴建立极坐标系. 曲线 的极坐标方程为 ， 为曲线 上异于极点的动点，点 在射线 上，且 成等比数列．
（Ⅰ）求点 的轨迹 的直角坐标方程；
（Ⅱ）已知 , 是曲线 上的一点且横坐标为 ，直线 与 交于 两点，试求 的值．

Answer 1

【答案】解：（I）设 ， ，
则由 成等比数列，可得 ，
即 ， ．
又 满足 ，即 ，
∴ ，
化为直角坐标方程为 .
（Ⅱ）依题意可得 ，故 ，即直线 倾斜角为 ，
∴直线 的参数方程为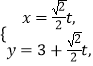
代入圆的直角坐标方程 ，
得 ，
故 ， ，
∴
【解析】本题考查的知识要点：参数方程和极坐标方程与直角坐标方程的转化，直线和圆的极坐标方程、参数方程等基础知识，考查数形结合思想、化归与转化思想等．曲线的极坐标方程定义：如果曲线C上的点与方程f（ρ，θ）=0有如下关系:
（1）曲线C上任一点的坐标（所有坐标中至少有一个）符合方程f（ρ，θ）=0；
（2）以方程f（ρ，θ）=0的所有解为坐标的点都在曲线C上．
则曲线C的方程是f（ρ，θ）=0．
【考点精析】通过灵活运用参数方程的定义，掌握在平面直角坐标系中，如果曲线上任意一点的坐标都是某个变数的函数并且对于的每一个允许值，由这个方程所确定的点都在这条曲线上，那么这个方程就叫做这条曲线的参数方程即可以解答此题．