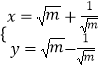题目内容
【题目】已知数列 
的前 
和为 
，若 
， 
．
（Ⅰ）求数列 的通项公式；
（Ⅱ）若 
，求数列 
的前 项和 
．
【答案】解：（Ⅰ） 
， 
．
当 
时， 
，得 
．
当 
时， 
，
，
，即 
，
．
数列 
是等差数列，且首项为 ，公差为2，
．
（Ⅱ）由（Ⅰ）可知， 
，
，——①
，——②
①–②得 
，
化简得 
．
解法二：（Ⅰ）同解法一.
（Ⅱ）由（Ⅰ）可知， ，
设 
，
解得 
，
∴ 
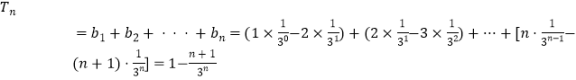
【解析】（Ⅰ）利用数列的递推关系式通过数列的第n项与前n项之间的关系an=Sn-Sn-1求数列{an}的通项公式；
（Ⅱ）利用错位相减法求解数列的和即可．或利用拆项法求解数列的和即可．本题考查数列的通项公式的求法，考查数列的前n项和公式的求法．
练习册系列答案
相关题目
