题目内容
已知圆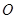 的方程为
的方程为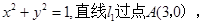 且与圆
且与圆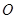 相切.
相切.
(1)求直线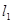 的方程;
的方程;
(2)设圆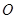 与
与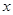 轴交于
轴交于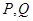 两点,M是圆
两点,M是圆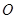 上异于
上异于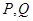 的任意一点,过点
的任意一点,过点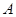 且与
且与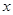 轴垂直的直线为
轴垂直的直线为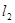 ,直线
,直线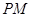 交直线
交直线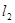 于点P’,直线
于点P’,直线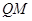 交直线
交直线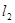 于点Q’
于点Q’
求证:以P’Q’为直径的圆 总过定点,并求出定点坐标.
总过定点,并求出定点坐标.
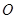 的方程为
的方程为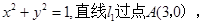 且与圆
且与圆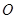 相切.
相切.(1)求直线
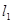 的方程;
的方程;(2)设圆
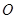 与
与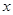 轴交于
轴交于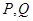 两点,M是圆
两点,M是圆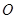 上异于
上异于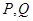 的任意一点,过点
的任意一点,过点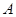 且与
且与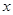 轴垂直的直线为
轴垂直的直线为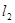 ,直线
,直线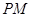 交直线
交直线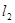 于点P’,直线
于点P’,直线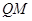 交直线
交直线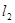 于点Q’
于点Q’求证:以P’Q’为直径的圆
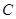 总过定点,并求出定点坐标.
总过定点,并求出定点坐标.(1) (2)定点坐标为
(2)定点坐标为
 (2)定点坐标为
(2)定点坐标为
(1)∵直线 过点
过点 ,且与圆
,且与圆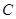 :
: 相切,
相切,
设直线 的方程为
的方程为 ,即
,即 , …………………………2分
, …………………………2分
则圆心 到直线
到直线 的距离为
的距离为 ,解得
,解得 ,
,
∴直线 的方程为
的方程为 ,即
,即 . …… …………………4分
. …… …………………4分
(2)对于圆方程 ,令
,令 ,得
,得 ,即
,即 .又直线
.又直线 过点
过点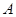 且与
且与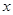 轴垂直,∴直线
轴垂直,∴直线 方程为
方程为 ,设
,设 ,则直线
,则直线 方程为
方程为
解方程组 ,得
,得 同理可得,
同理可得, ……………… 8分
……………… 8分
∴以 为直径的圆
为直径的圆 的方程为
的方程为 ,
,
又 ,∴整理得
,∴整理得 ,……………………… 10分
,……………………… 10分
若圆 经过定点,只需令
经过定点,只需令 ,从而有
,从而有 ,解得
,解得 ,
,
∴圆 总经过定点坐标为
总经过定点坐标为 . ……………………………………………12分
. ……………………………………………12分
 过点
过点 ,且与圆
,且与圆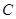 :
: 相切,
相切,设直线
 的方程为
的方程为 ,即
,即 , …………………………2分
, …………………………2分则圆心
 到直线
到直线 的距离为
的距离为 ,解得
,解得 ,
,∴直线
 的方程为
的方程为 ,即
,即 . …… …………………4分
. …… …………………4分(2)对于圆方程
 ,令
,令 ,得
,得 ,即
,即 .又直线
.又直线 过点
过点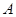 且与
且与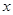 轴垂直,∴直线
轴垂直,∴直线 方程为
方程为 ,设
,设 ,则直线
,则直线 方程为
方程为
解方程组
 ,得
,得 同理可得,
同理可得, ……………… 8分
……………… 8分∴以
 为直径的圆
为直径的圆 的方程为
的方程为 ,
, 又
 ,∴整理得
,∴整理得 ,……………………… 10分
,……………………… 10分若圆
 经过定点,只需令
经过定点,只需令 ,从而有
,从而有 ,解得
,解得 ,
,∴圆
 总经过定点坐标为
总经过定点坐标为 . ……………………………………………12分
. ……………………………………………12分
练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
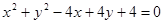 上有四点到直线
上有四点到直线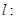
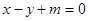 的距离为
的距离为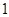 ,则
,则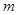 的取值范围为______________.
的取值范围为______________.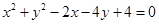 相交所得弦的长为2,则该直线的方程为________;
相交所得弦的长为2,则该直线的方程为________; 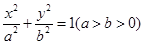 的左、右焦点分别是
的左、右焦点分别是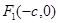 、
、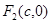 ,离心率为
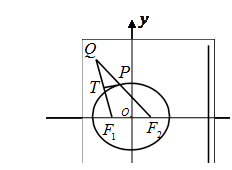
,离心率为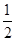 ,椭圆上的动点
,椭圆上的动点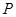 到直线
到直线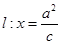 的最小距离为2,延长
的最小距离为2,延长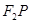 至
至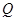 使得
使得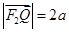 ,线段
,线段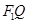 上存在异于
上存在异于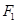 的点
的点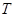 满足
满足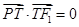 .
.
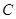 的方程;
的方程;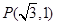 且与圆
且与圆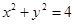 相切的直线方程 ___.
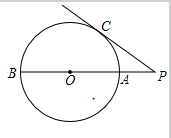
相切的直线方程 ___.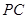 切圆
切圆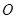 于点
于点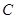 ,割线
,割线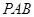 经过圆心
经过圆心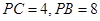 ,则
,则 .
. 
 上一点
上一点 的切线方程是____________.
的切线方程是____________.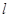 被圆
被圆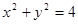 截得的弦长为2,则直线
截得的弦长为2,则直线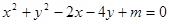 ,
,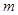 的取值范围;
的取值范围;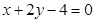 相交于
相交于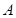 、
、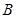 两点,且
两点,且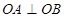 (
(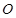 为坐标原点),求
为坐标原点),求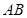 为直径的圆的方程。
为直径的圆的方程。