题目内容
已知椭圆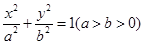 的左、右焦点分别是
的左、右焦点分别是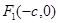 、
、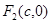 ,离心率为
,离心率为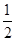 ,椭圆上的动点
,椭圆上的动点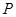 到直线
到直线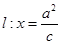 的最小距离为2,延长
的最小距离为2,延长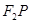 至
至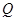 使得
使得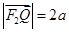 ,线段
,线段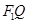 上存在异于
上存在异于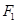 的点
的点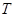 满足
满足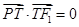 .
.
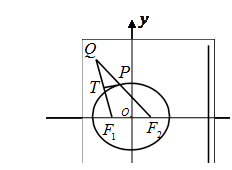
(1) 求椭圆的方程;
(2) 求点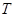 的轨迹
的轨迹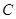 的方程;
的方程;
(3) 求证:过直线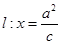 上任意一点必可以作两条直线
上任意一点必可以作两条直线
与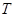 的轨迹
的轨迹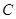 相切,并且过两切点的直线经过定点.
相切,并且过两切点的直线经过定点.
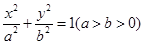 的左、右焦点分别是
的左、右焦点分别是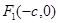 、
、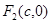 ,离心率为
,离心率为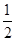 ,椭圆上的动点
,椭圆上的动点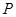 到直线
到直线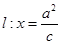 的最小距离为2,延长
的最小距离为2,延长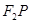 至
至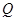 使得
使得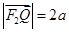 ,线段
,线段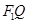 上存在异于
上存在异于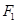 的点
的点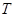 满足
满足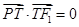 .
.
(1) 求椭圆的方程;
(2) 求点
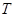 的轨迹
的轨迹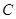 的方程;
的方程;(3) 求证:过直线
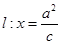 上任意一点必可以作两条直线
上任意一点必可以作两条直线与
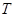 的轨迹
的轨迹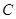 相切,并且过两切点的直线经过定点.
相切,并且过两切点的直线经过定点. (1)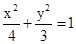 ;(2)
;(2)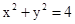 ;(3)直线经过定点(1,0).
;(3)直线经过定点(1,0).
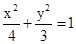 ;(2)
;(2)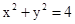 ;(3)直线经过定点(1,0).
;(3)直线经过定点(1,0).本试题主要考查了圆与直线,以及椭圆的方程,直线与椭圆的位置关系的综合运用。
解:(1)依题意得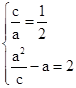 , ………………………………………………2分
, ………………………………………………2分
解得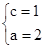 ,∴
,∴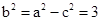 ……………………………………………………………3分
……………………………………………………………3分
椭圆的方程为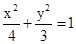 …………………………………………………………………4分
…………………………………………………………………4分
(2)解法1:设点T的坐标为(x,y).
当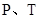 重合时,点
重合时,点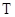 坐标为
坐标为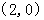 和点
和点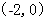 , …………………………………5分
, …………………………………5分
当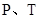 不重合时,由
不重合时,由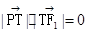 ,得
,得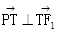 . ……………………………6分
. ……………………………6分
由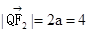 及椭圆的定义,
及椭圆的定义,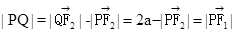 , …………7分
, …………7分
所以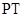 为线段
为线段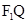 的垂直平分线,T为线段
的垂直平分线,T为线段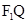 的中点
的中点
在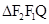 中,
中,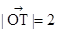 , …………………………………………8分
, …………………………………………8分
所以有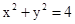 .
.
综上所述,点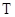 的轨迹C的方程是
的轨迹C的方程是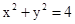 . …………………………………9分
. …………………………………9分
(3) 直线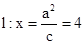 与
与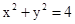 相离,
相离,
过直线上任意一点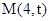 可作圆
可作圆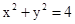 的两条切线
的两条切线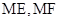 …………10分
…………10分
所以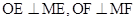
所以O,E,M,F四点都在以OM为直径的圆上, …………………………11分
其方程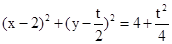 ④ …………………………12分
④ …………………………12分
EF为两圆的公共弦,③-④得:EF的方程为4X+ty -4=0 ………13分
显然无论t为何值,直线ef经过定点(1,0). ………………14分
解:(1)依题意得
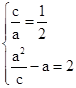 , ………………………………………………2分
, ………………………………………………2分解得
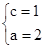 ,∴
,∴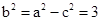 ……………………………………………………………3分
……………………………………………………………3分椭圆的方程为
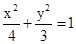 …………………………………………………………………4分
…………………………………………………………………4分(2)解法1:设点T的坐标为(x,y).
当
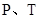 重合时,点
重合时,点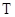 坐标为
坐标为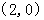 和点
和点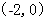 , …………………………………5分
, …………………………………5分当
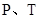 不重合时,由
不重合时,由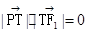 ,得
,得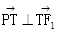 . ……………………………6分
. ……………………………6分由
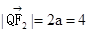 及椭圆的定义,
及椭圆的定义,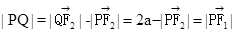 , …………7分
, …………7分所以
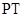 为线段
为线段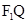 的垂直平分线,T为线段
的垂直平分线,T为线段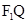 的中点
的中点在
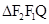 中,
中,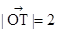 , …………………………………………8分
, …………………………………………8分所以有
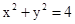 .
.综上所述,点
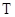 的轨迹C的方程是
的轨迹C的方程是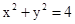 . …………………………………9分
. …………………………………9分(3) 直线
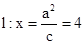 与
与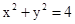 相离,
相离,过直线上任意一点
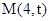 可作圆
可作圆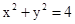 的两条切线
的两条切线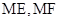 …………10分
…………10分所以
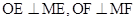
所以O,E,M,F四点都在以OM为直径的圆上, …………………………11分
其方程
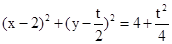 ④ …………………………12分
④ …………………………12分EF为两圆的公共弦,③-④得:EF的方程为4X+ty -4=0 ………13分
显然无论t为何值,直线ef经过定点(1,0). ………………14分

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
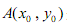 是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.
是曲线C上的一个定点,过点A任意作两条倾斜角互补的直线,分别与曲线C相交于另外两点P 、Q.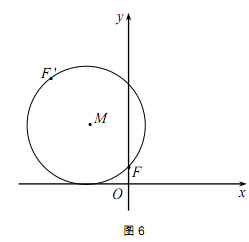
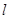 :
: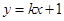 (k
(k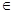 R)与圆C:
R)与圆C: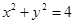 相交于点A、B, M为弦AB中点.
相交于点A、B, M为弦AB中点.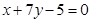 截圆
截圆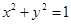 所得的两段弧长之差的绝对值是
所得的两段弧长之差的绝对值是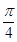

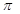
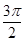
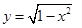 与直线
与直线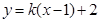 有两个交点时,实数
有两个交点时,实数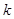 的取值范围是( )
的取值范围是( )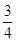 ≤k<1
≤k<1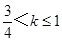
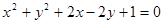 关于直线
关于直线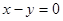 对称的圆的方程为 .
对称的圆的方程为 .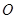 的方程为
的方程为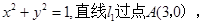 且与圆
且与圆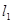 的方程;
的方程;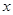 轴交于
轴交于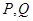 两点,M是圆
两点,M是圆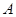 且与
且与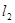 ,直线
,直线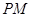 交直线
交直线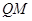 交直线
交直线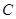 总过定点,并求出定点坐标.
总过定点,并求出定点坐标.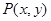 是圆
是圆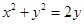 上的动点, (13分)
上的动点, (13分)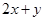 的取值范围
的取值范围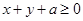 恒成立,求实数
恒成立,求实数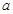 的取值。
的取值。 与圆
与圆 交于
交于 两点,且
两点,且 ,则实数
,则实数 的值为( )
的值为( ) 或
或