题目内容
已知点M到F(
,0)的距离比它到y轴的距离大
,求点M的轨迹方程.
| 1 |
| 2 |
| 1 |
| 2 |
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:设出M坐标(x,y),当x≥0时由题意列出满足条件的等式,化简后得到M的轨迹方程;再由题意得到x轴负半轴上的点也满足条件.两种情况结合一起得到点M的轨迹方程.
解答:
解:设M(x,y),
则|MF|=
,
当x≥0时,
M到y轴的距离为x.
由点M到F(
,0)的距离比它到y轴的距离大
,得
=x+
.
两边平方并整理得:y2=2x;
当x<0时,由题意可得M的轨迹为y=0(x<0),此时符合题意.
综上,点M的轨迹方程为y2=2x或y=0(x<0).
则|MF|=
(x-
|
当x≥0时,
M到y轴的距离为x.
由点M到F(
| 1 |
| 2 |
| 1 |
| 2 |
(x-
|
| 1 |
| 2 |
两边平方并整理得:y2=2x;
当x<0时,由题意可得M的轨迹为y=0(x<0),此时符合题意.
综上,点M的轨迹方程为y2=2x或y=0(x<0).
点评:本题考查了轨迹方程的求法,解答此题的关键是不要漏掉x轴负半轴,是中档题也是易错题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
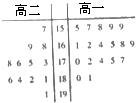 某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.
某学校为准备参加市运动会,对本校高一、高二两个田径队中30名跳高运动员进行了测试,并用茎叶图表示出本次测试30人的跳高成绩(单位:cm).跳高成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下定义为“不合格”.