题目内容
【题目】将一铁块高温融化后制成一张厚度忽略不计、面积为100dm2的矩形薄铁皮(如图),并沿虚线l1,l2裁剪成A,B,C三个矩形(B,C全等),用来制成一个柱体.现有两种方案:
方案①:以![]() 为母线,将A作为圆柱的侧面展开图,并从B,C中各裁剪出一个圆形作为圆柱的两个底面;
为母线,将A作为圆柱的侧面展开图,并从B,C中各裁剪出一个圆形作为圆柱的两个底面;
方案②:以![]() 为侧棱,将A作为正四棱柱的侧面展开图,并从B,C中各裁剪出一个正方形(各边分别与
为侧棱,将A作为正四棱柱的侧面展开图,并从B,C中各裁剪出一个正方形(各边分别与![]() 或
或![]() 垂直)作为正四棱柱的两个底面.
垂直)作为正四棱柱的两个底面.
(1)设B,C都是正方形,且其内切圆恰为按方案①制成的圆柱的底面,求底面半径;
(2)设![]() 的长为
的长为![]() dm,则当
dm,则当![]() 为多少时,能使按方案②制成的正四棱柱的体积最大?
为多少时,能使按方案②制成的正四棱柱的体积最大?

【答案】(1) 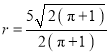 ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)设所得圆柱的半径为![]() ,根据矩形薄铁皮的面积为100
,根据矩形薄铁皮的面积为100![]() ,即可求得
,即可求得![]() 的值;(2)设所得正四棱柱的底面边长为
的值;(2)设所得正四棱柱的底面边长为![]()
![]() ,根据题意得
,根据题意得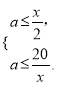 .方法一:表示出正四棱柱的体积
.方法一:表示出正四棱柱的体积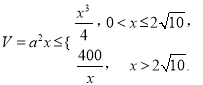 ,构造函数,求得单调性,即可求得函数的最大值,从而得体积最大值及
,构造函数,求得单调性,即可求得函数的最大值,从而得体积最大值及![]() 的值;方法二:表示出
的值;方法二:表示出![]() 的范围,从而得到
的范围,从而得到![]() 的范围,再表示出正四棱柱的体积,即可求得最大值及
的范围,再表示出正四棱柱的体积,即可求得最大值及![]() 的值.
的值.
试题解析:(1)设所得圆柱的半径为![]() ,则
,则![]() ,
,
解得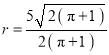 .
.
(2)设所得正四棱柱的底面边长为![]() dm,则
dm,则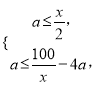 即
即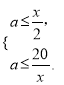
方法一:
所得正四棱柱的体积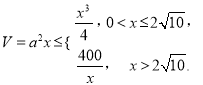
记函数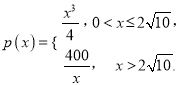 则
则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∴当![]() 时,
时, ![]() .
.
∴当![]() ,
, ![]() 时,
时, ![]()
![]() dm3.
dm3.
方法二:
![]() ,从而
,从而![]() .
.
所得正四棱柱的体积![]() .
.
∴当![]() ,
, ![]() 时,
时, ![]()
![]() dm3.
dm3.
答:(1)圆柱的底面半径为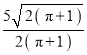 dm;
dm;
(2)当![]() 为
为![]() 时,能使按方案②制成的正四棱柱的体积最大.
时,能使按方案②制成的正四棱柱的体积最大.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】下表为![]() 年至
年至![]() 年某百货零售企业的线下销售额(单位:万元),其中年份代码
年某百货零售企业的线下销售额(单位:万元),其中年份代码![]() 年份
年份![]() .
.
年份代码 |
|
|
|
|
线下销售额 |
|
|
|
|
(1)已知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程,并预测
的线性回归方程,并预测![]() 年该百货零售企业的线下销售额;
年该百货零售企业的线下销售额;
(2)随着网络购物的飞速发展,有不少顾客对该百货零售企业的线下销售额持续增长表示怀疑,某调查平台为了解顾客对该百货零售企业的线下销售额持续增长的看法,随机调查了![]() 位男顾客、
位男顾客、![]() 位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有
位女顾客(每位顾客从“持乐观态度”和“持不乐观态度”中任选一种),其中对该百货零售企业的线下销售额持续增长持乐观态度的男顾客有![]() 人、女顾客有
人、女顾客有![]() 人,能否在犯错误的概率不超过
人,能否在犯错误的概率不超过![]() 的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
的前提下认为对该百货零售企业的线下销售额持续增长所持的态度与性别有关?
参考公式及数据:
 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|


