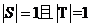题目内容
设a＞1，0＜b＜1，则logab+logba的取值范围为（ ）
| A、[2，+∞） | B、（2，+∞） | C、（-∞，-2） | D、（-∞，-2] |
分析：换元，令t=logab＜0，-t＞0，使用基本不等式．
解答：解：∵a＞1，0＜b＜1，∴logab＜0，logba=
＜0.
设logab=t，logba=
，则-t+
≥2；
则logab+logba=t+
=-(-t+
)≤-2；
故选D．
| 1 |
| logab |
设logab=t，logba=
| 1 |
| t |
| 1 |
| -t |
则logab+logba=t+
| 1 |
| t |
| 1 |
| -t |
故选D．
点评：体现整体换元的数学思想．
练习册系列答案
科学实验活动册系列答案
相关题目
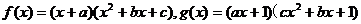.记集合S=
若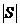
，
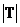分别为集合元素S，T的元素个数，则下列结论不可能的是