题目内容
(
唐山五校模拟)如下图,四棱锥P-ABCD的底面是直角梯形,∠ADC=∠DCB=90°,AD=1,BC=3.PC=CD=2,PC⊥底面ABCD,E为AB的中点.(1)
求证:平面PDE⊥平面PAC;(2)
求直线PC与平面PDE所成的角;(3)
求点B到平面PDE的距离.
答案:略
解析:
解析:
|
解析:建立如图所示的坐标系 C-xyz,则C(0,0,0)、A(2,1,0)、B(0,3,0)、P(0,0,2),D(2,0,0)、E(1,2,0).(1)
又  平面PDE, 平面PDE,
∴平面 PDE⊥平面PAC. (4分)
(2) 设n=(x,y,z)为面PDE的法向量,则 , ,
由于  , ,
 , ,
设直线 PC与平面PDE所成的角为θ,而 , ,
所以  ,即直线PC与平面PDE所成的角为 ,即直线PC与平面PDE所成的角为 . (8分) . (8分)
(3) 因为 ,所以点B到平面PDE的距离 ,所以点B到平面PDE的距离 . (12分) . (12分) |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(2007
湖北八校模拟)如下图,△PAB所在的平面α和四边形ABCD所在的平面β垂直,且AD⊥α,BC⊥α,AD=4,BC=8,AB=6,∠APD=∠CPB,则点P在平面α内的轨迹是
[
]|
A .圆的一部分 |
B .椭圆的一部分 |
|
C .双曲线的一部分 |
D .抛物线的一部分 |







 -
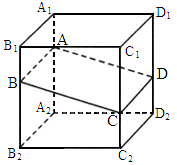
-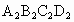 的棱长为a,A、B、C、D分别在
的棱长为a,A、B、C、D分别在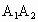 、
、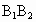 、
、 、
、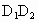 上,且
上,且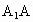 =
=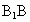 =
=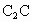 =
=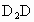 =
=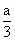 ,则四边形ABCD的面积为
,则四边形ABCD的面积为
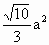
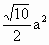
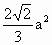
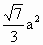
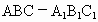 中,∠ACB=90°,
中,∠ACB=90°,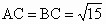 ,
,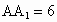 ,E、F分别为
,E、F分别为 与
与 的中点.
的中点.
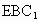 与平面ABC所成的锐二面角的大小.
与平面ABC所成的锐二面角的大小.
