题目内容
设定义在R上的偶函数 满足
满足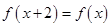 ,
,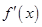 是
是 的导函数,当
的导函数,当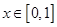 时,
时,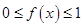 ;当
;当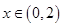 且
且 时,
时,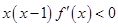 .则方程
.则方程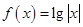 根的个数为( )
根的个数为( )
| A.12 | B.1 6 | C.18 | D.20 |
C
解析试题分析:函数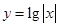 的图像如图所示:
的图像如图所示:
可知函数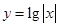 在区间
在区间 和
和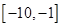 上的图像在直线
上的图像在直线 与直线
与直线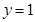 之间.由
之间.由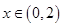 且
且 时,
时,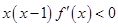 可知,函数
可知,函数 在区间
在区间 上是单调递增的,在区间
上是单调递增的,在区间 上的单调递减的,又因为当
上的单调递减的,又因为当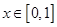 时,
时,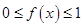 ,且已知函数是周期为
,且已知函数是周期为 的偶函数,所以已知函数在区间
的偶函数,所以已知函数在区间 上的图像在直线
上的图像在直线 与直线
与直线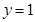 之间,与函数
之间,与函数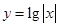 的图像在区间
的图像在区间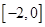 与
与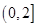 上分别有1个交点,在区间
上分别有1个交点,在区间 ,
,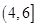 ,
,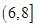 ,
, ,
, ,
, ,
,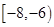 ,
,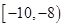 上分别有2个交点,所以一共有18个交点,即方程
上分别有2个交点,所以一共有18个交点,即方程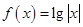 根的个数为
根的个数为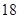 .
.
考点:1.对数函数的图形与性质;2.函数单调性与导数的关系;3.数形结合思想

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
已知奇函数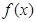 在
在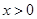 时,
时,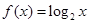 ,则
,则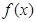 在区间
在区间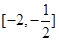 的值域为( )
的值域为( )
A.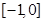 | B.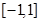 | C.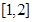 | D.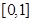 |
函数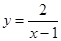 的定义域是
的定义域是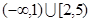 ,则其值域为( )
,则其值域为( )
A.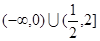 | B.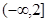 |
C.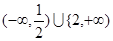 | D. |
定义在 上的函数
上的函数 满足
满足 ,当
,当 时,
时, ,当
,当 时,
时,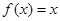 .则
.则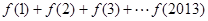 =( )
=( )
| A.338 | B.337 | C.1678 | D.2013 |
下列函数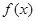 中,满足“对任意
中,满足“对任意 ,
,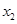
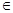 (0,
(0,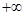 ),当
),当 <
<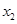 时,
时,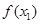 >
>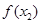 的是 ( )
的是 ( )
A.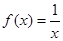 | B.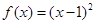 | C.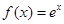 | D.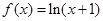 |
已知函数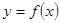 是R上的偶函数,且
是R上的偶函数,且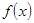 在
在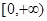 上是减函数,若
上是减函数,若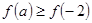 ,则
,则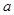 的取值范围是( )
的取值范围是( )
A.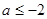 | B.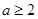 | C.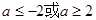 | D.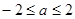 |
已知函数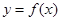 为
为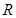 上的减函数,则满足
上的减函数,则满足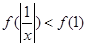 的实数
的实数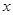 的取值范围是( )
的取值范围是( )
A.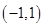  | B.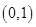 | C.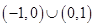 | D.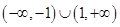 |
若定义在R上的偶函数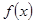 满足
满足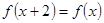 且
且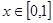 时,
时,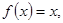 则方程
则方程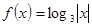 的零点个数是( )
的零点个数是( )
| A.2个 | B.3个 | C.4个 | D.多于4个 |
设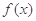 是定义在
是定义在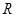 上的偶函数,且在
上的偶函数,且在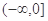 上是增函数,设
上是增函数,设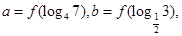
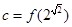 ,则
,则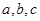 的大小关系是( )
的大小关系是( )
A.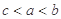 | B.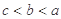 | C.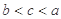 | D.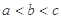 |