题目内容
若定义在R上的偶函数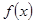 满足
满足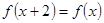 且
且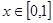 时,
时,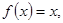 则方程
则方程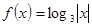 的零点个数是( )
的零点个数是( )
| A.2个 | B.3个 | C.4个 | D.多于4个 |
C
解析试题分析:由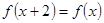 知,函数
知,函数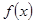 是周期为2的周期函数,且是偶函数,在同一坐标系中画出
是周期为2的周期函数,且是偶函数,在同一坐标系中画出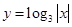 和
和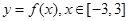 的图像,有图可知零点个数为4个.
的图像,有图可知零点个数为4个.
考点:1、周期函数;2、函数的图像;3、函数的零点.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
实数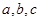 是图象连续不断的函数
是图象连续不断的函数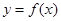 定义域中的三个数,且满足
定义域中的三个数,且满足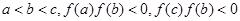 ,则
,则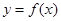 在区间
在区间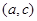 的零点个数为( )
的零点个数为( )
| A.2 | B.奇数 | C.偶数 | D.至少是2 |
设定义在R上的偶函数 满足
满足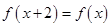 ,
,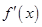 是
是 的导函数,当
的导函数,当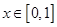 时,
时,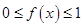 ;当
;当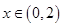 且
且 时,
时,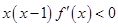 .则方程
.则方程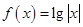 根的个数为( )
根的个数为( )
| A.12 | B.1 6 | C.18 | D.20 |
对函数f(x)=1-(x∈R)的如下研究结果,正确的是 ( )
A. 既不是奇函数又不是偶函数. 既不是奇函数又不是偶函数. |
B. 既是奇函数又是偶函数. 既是奇函数又是偶函数. |
C. 是偶函数但不是奇函数. 是偶函数但不是奇函数. |
D. 是奇函数但不是偶函数. 是奇函数但不是偶函数. |
下列函数中,在区间(0,+∞)上是减函数的是( )
A. | B.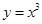 | C. | D. |
下列4个函数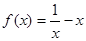 ,
,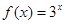 ,
,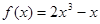 ,
,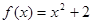 中,奇函数的个数是 ( )
中,奇函数的个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
设函数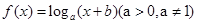 的图像过点
的图像过点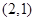 ,其反函数的图像过点
,其反函数的图像过点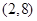 ,则
,则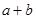 等于 ( )
等于 ( )
| A.1 | B.2 | C.3 | D.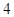 |
下列函数在定义域上既是奇函数又是增函数的为( )
A.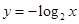 | B.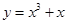 | C.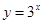 | D.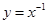 |
函数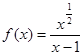 的定义域( )
的定义域( )
A.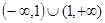 | B.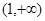 |
C.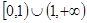 | D.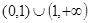 |