题目内容
17.定义符号max{a,b}的含义为:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{2,-3}=2,max{-4,-2}=-2,则max{x2+x-2,2x}的最小值是( )| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | -2 | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | 4 |
分析 设f(x)=max{x2+x-2,2x},由定义讨论当x2+x-2≥2x,当x2+x-2<2x,求得f(x),运用二次函数和一次函数的单调性,可得最小值.
解答 解:设f(x)=max{x2+x-2,2x},
当x2+x-2≥2x,即x≥2或x≤-1时,f(x)=x2+x-2,
由于对称轴x=-$\frac{1}{2}$,可得f(x)在x≥2递增,可得f(x)≥f(2)=4,
f(x)在x≤-1递减,可得f(x)≥f(-1)=-2;
当x2+x-2<2x,即-1<x<2时,f(x)=2x,
可得f(x)在-1<x<2递增,即有-2<f(x)<4,
综上可得,f(x)的值域为[-2,+∞),
即有f(x)=max{x2+x-2,2x}的最小值为-2.
故选B.
点评 本题考查新定义的理解和运用,考查二次不等式的解法,考查二次函数和一次函数的最值的求法,属于中档题.

练习册系列答案
相关题目
8.结论“对任意的x∈[1,2],x2-a≤0恒成立”成立的一个充分不必要条件是( )
| A. | a≥4 | B. | a≥5 | C. | a≤4 | D. | a≤5 |
5.已知一组数据为1、5、6、2、6,则这组数据的众数、中位数、平均数的大小关系为( )
| A. | 中位数>平均数>众数 | B. | 众数>中位数>平均数 | ||
| C. | 众数>平均数>中位数 | D. | 平均数>众数>中位数 |
12.设关于x、y的不等式组$\left\{\begin{array}{l}{x+y-1≥0}\\{x-1≤0}\\{ax-y+1≥0}\end{array}\right.$表示的平面区域内存在点P(x0,y0),满足2x0+y0=4,则a的取值范围是( )
| A. | (-∞,-2)∪[1,+∞) | B. | (-∞,-2) | C. | (-2,1] | D. | [1,+∞) |
6.不等式-25x2+10x-1≥0的解集为( )
| A. | ∅ | B. | $\left\{{x\left|{x=\frac{1}{5}}\right.}\right\}$ | C. | $\left\{{x\left|{x≠\frac{1}{5}}\right.}\right\}$ | D. | $\left\{{x\left|{x≤\frac{1}{5}}\right.}\right\}$ |
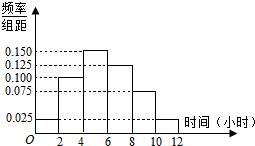 某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).
某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).