题目内容
3.已知极坐标系的极点在直角坐标系的原点,极轴与x轴的正半轴重合,直线l的极坐标方程为$ρsin(θ+\frac{π}{4})=2\sqrt{2}$.在直角坐标系中,曲线C的参数方程为$\left\{\begin{array}{l}x=2+\sqrt{3}cosθ\\ y=sinθ\end{array}$(θ为参数).求曲线C上的点到直线l的距离的最大值及相应点的坐标.分析 直线l的极坐标方程化为普通方程,设出曲线C的点的坐标,利用点到直线的距离公式得到关系式,然后求解即可.
解答 解:直线l的直角坐标方程为x+y-4=0
设曲线C上点P的坐标为$(2+\sqrt{3}cosθ,sinθ)$,
∴P点到直线l:x+y-4=0的距离$d=\frac{{|2+\sqrt{3}cosθ+sinθ-4|}}{{\sqrt{2}}}=\frac{{|\sqrt{3}cosθ+sinθ-2|}}{{\sqrt{2}}}=\frac{{|2sin(θ+\frac{π}{3})-2|}}{{\sqrt{2}}}$
当且仅当$sin(θ+\frac{π}{3})=-1$,即$θ+\frac{π}{3}=-\frac{π}{2}+2kπ$,$θ=2kπ-\frac{5π}{6}(k∈Z)$时,d取得最大值$2\sqrt{2}$,此时$cosθ=cos(2kπ-\frac{5π}{6})=-\frac{{\sqrt{3}}}{2},sinθ=sin(2kπ-\frac{5π}{6})=-\frac{1}{2}$
即$P(\frac{1}{2},-\frac{1}{2})$
故曲线C上的点到直线l的距离的最大值为$2\sqrt{2}$,相应点的坐标为$(\frac{1}{2},-\frac{1}{2})$.
点评 本题考查直线的极坐标方程与普通方程的互化,点到直线的距离以及三角函数的最值的求法,考查计算能力.

练习册系列答案
相关题目
14.设x,y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$,目标函数z=x+2y的最小值是( )
| A. | 11 | B. | 9 | C. | 5 | D. | 1 |
11.y=cos2x-$\frac{1}{2}$是( )
| A. | 最小正周期为2π的偶函数 | B. | 最小正周期为2π的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为π的奇函数 |
18.在两个变量y与x的回归模型中,分别选择了四个不同的模型,且它们的R2的值的大小关系为:R${\;}_{模型3}^{2}$<R${\;}_{模型4}^{2}$<R${\;}_{模型1}^{2}$<R${\;}_{模型2}^{2}$,则拟合效果最好的是( )
| A. | 模型1 | B. | 模型2 | C. | 模型3 | D. | 模型4 |
15.如果a,b,c满足c<b<a且ac<0,那么下列选项中不一定成立的是( )
| A. | $\frac{b}{a}>\frac{c}{a}$ | B. | c(b-a)>0 | C. | ac(a-c)<0 | D. | cb2<ab2 |
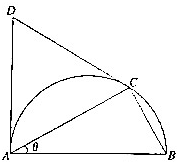 如图是一个半径为1的半圆,AB是直径,点C在圆弧上,且与A、B不重合,△ACD是等边三角形,设∠CAB=θ(0<θ<$\frac{π}{2}$),
如图是一个半径为1的半圆,AB是直径,点C在圆弧上,且与A、B不重合,△ACD是等边三角形,设∠CAB=θ(0<θ<$\frac{π}{2}$),