题目内容
19.下列说法正确的是①④①已知定点F1(-1,0)、F2(1,0),则满足||PF1|-|PF2||=3的动点P的轨迹不存在;
②若动点P到定点F的距离等于动点P到定直线l的距离,则动点P的轨迹为抛物线;
③命题“?x<0,都有x-x2<0”的否定为“?x0≥0,使得${x_0}-{x_0}^2≥0$”;
④已知定点F1(-2,0)、F2(2,0),则满足|PF1|+|PF2|=4的动点P的轨迹为线段F1F2;
⑤$\frac{x^2}{m}-\frac{y^2}{n}=1({mn>0})$表示焦点在x轴上的双曲线.
分析 由构成三角形的条件,两边之差小于第三边,即可判断①;由抛物线的定义,即可判断②;
由命题的否定形式,即可判断③;由构成三角形或线段的条件,判断④;
讨论m>0,n>0或m<0,n<0,即可判断⑤.
解答 解:①定点F1(-1,0)、F2(1,0),|F1F2|=2,
则满足||PF1|-|PF2||=3>2的动点P的轨迹不存在,故①正确;
②若动点P到定点F的距离等于动点P到定直线l的距离,若F在直线l上,可得P的轨迹为过F垂直于l的直线,
则动点P的轨迹为抛物线错,故②错误;
③命题“?x<0,都有x-x2<0”的否定为“?x0<0,使得${x_0}-{x_0}^2≥0$”故③错误;
④定点F1(-2,0)、F2(2,0),则满足|PF1|+|PF2|=4=|F1F2|的动点P的轨迹为线段F1F2,故④正确;
⑤$\frac{x^2}{m}-\frac{y^2}{n}=1({mn>0})$,当m>0,n>0表示焦点在x轴上的双曲线,当m<0,n<0表示焦点在y轴上的双曲线,
故⑤错误.
故答案为:①④.
点评 本题考查命题的真假判断和应用,主要是圆锥曲线的定义和命题的否定,注意定义满足的条件是解题的关键,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知实数x,y满足不等式组$\left\{{\begin{array}{l}{x+y-2≤0}\\{x-y≤0}\\{x≥-3}\end{array}}\right.$,则z=x+3y+7的最大值为( )
| A. | -5 | B. | 11 | C. | 15 | D. | 19 |
9.已知在极坐标系中,点A(2,$\frac{π}{2}$),B($\sqrt{2}$,$\frac{3π}{4}$),O(0,0),则△ABO为( )
| A. | 正三角形 | B. | 直角三角形 | C. | 等腰锐角三角形 | D. | 等腰直角三角形 |
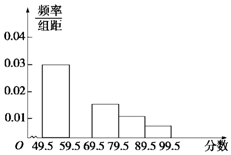 在长丰中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.
在长丰中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.