题目内容
 现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值.
现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值.分析:表示出四边形OAPB,利用二倍角公式及辅助角公式化简函数,结合角的范围,确定面积的最大值.
解答:解:由题意,f(θ)=SOAPB=
(|OB|+|AP|)•|OA|=
(
cosθ+sinθ)•cosθ …(4分)
=
(
cos2θ+sinθ•cosθ)=
(
+
sin2θ)=
sin(2θ+
)+
…(8分)
又∵0<θ<
,∴
<2θ+
<
,∴2θ+
=
∴θ=
时,面积f(θ)取最大值
…(12分)
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
=
| 1 |
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
| 1+cos2θ |
| 2 |
| 1 |
| 2 |
| ||
| 6 |
| π |
| 6 |
| ||
| 12 |
又∵0<θ<
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| π |
| 2 |
∴θ=
| π |
| 6 |
| ||
| 4 |
点评:本题考查面积的计算,考查三角函数的化简,考查三角函数的最值,确定函数解析式是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
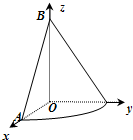 如图,直角三角形OAB的直角顶点O是空间坐标系O-xyz的原点,点A在Ox轴正半轴上,|OA|=1;点B在Oz轴正半轴上,|OB|=2.我们称△OAB绕Oz轴逆时针旋转
如图,直角三角形OAB的直角顶点O是空间坐标系O-xyz的原点,点A在Ox轴正半轴上,|OA|=1;点B在Oz轴正半轴上,|OB|=2.我们称△OAB绕Oz轴逆时针旋转| π |
| 2 |
| A、该四分之一圆锥体主视图和左视图的图形是全等的直角三角形 | ||
B、该四分之一圆锥体俯视图的图形是一个圆心角为
| ||
| C、该四分之一圆锥体主视图、左视图和俯视图的图形都是扇形 | ||
| D、该四分之一圆锥体主视图的图形面积大于俯视图的图形面积 |
 现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值.
现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值. ,圆半径为
,圆半径为 ,要裁剪成四边形
,要裁剪成四边形 ,且满足
,且满足 ,
, ,
, ,记此四边形的面积为
,记此四边形的面积为 ,求
,求