题目内容
 现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值.
现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值.
解:由题意,f(θ)= =
= …(4分)
…(4分)
= =
= =
= …(8分)
…(8分)
又∵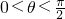 ,∴
,∴ ,∴
,∴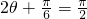
∴ 时,面积f(θ)取最大值
时,面积f(θ)取最大值 …(12分)
…(12分)
分析:表示出四边形OAPB,利用二倍角公式及辅助角公式化简函数,结合角的范围,确定面积的最大值.
点评:本题考查面积的计算,考查三角函数的化简,考查三角函数的最值,确定函数解析式是关键.
 =
= …(4分)
…(4分)=
 =
= =
= …(8分)
…(8分)又∵
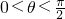 ,∴
,∴ ,∴
,∴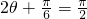
∴
 时,面积f(θ)取最大值
时,面积f(θ)取最大值 …(12分)
…(12分)分析:表示出四边形OAPB,利用二倍角公式及辅助角公式化简函数,结合角的范围,确定面积的最大值.
点评:本题考查面积的计算,考查三角函数的化简,考查三角函数的最值,确定函数解析式是关键.

练习册系列答案
相关题目
 现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值.
现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值. ,圆半径为
,圆半径为 ,要裁剪成四边形
,要裁剪成四边形 ,且满足
,且满足 ,
, ,
, ,记此四边形的面积为
,记此四边形的面积为 ,求
,求