题目内容
17.已知x=$\frac{π}{3}$是函数f(x)=(b-$\sqrt{3}a$)sinx+(a-b)cosx(a≠0)的一个零点,则函数g(x)=asinx-bcosx的图象可能是( )| A. | 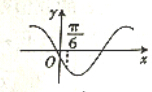 | B. | 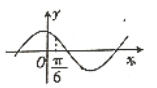 | ||
| C. | 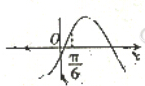 | D. | 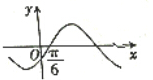 |
分析 由题意知f($\frac{π}{3}$)=(b-$\sqrt{3}a$)sin$\frac{π}{3}$+(a-b)cos$\frac{π}{3}$=0,从而解得a=$\frac{\sqrt{3}-1}{2}$b,(b≠0),从而可得g(0)=-b,g($\frac{π}{6}$)=-$\frac{\sqrt{3}+1}{4}$b,从而确定答案.
解答 解:∵x=$\frac{π}{3}$是函数f(x)=(b-$\sqrt{3}a$)sinx+(a-b)cosx(a≠0)的一个零点,
∴f($\frac{π}{3}$)=(b-$\sqrt{3}a$)sin$\frac{π}{3}$+(a-b)cos$\frac{π}{3}$=0,
即(b-$\sqrt{3}a$)$\frac{\sqrt{3}}{2}$+(a-b)$\frac{1}{2}$=0,
即a=$\frac{\sqrt{3}-1}{2}$b,(b≠0),
故g(x)=$\frac{\sqrt{3}-1}{2}$bsinx-bcosx,
故g(0)=-b,g($\frac{π}{6}$)=$\frac{\sqrt{3}-1}{2}$b$\frac{1}{2}$-b$\frac{\sqrt{3}}{2}$=-$\frac{\sqrt{3}+1}{4}$b,
故g(0)与g($\frac{π}{6}$)同号,且|g(0)|>|g($\frac{π}{6}$)|;
故选:B.
点评 本题考查了函数的零点的应用及函数的图象的应用,属于中档题.

练习册系列答案
相关题目
7.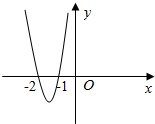 已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )
已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )
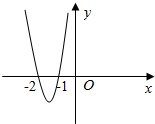 已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )
已知函数f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )| A. | {x|-2<x<-1,或1<x<2} | B. | {x|-2<x<-1,或0<x<1,或x>2} | ||
| C. | {x|x<-2,或1<x<2} | D. | {x|x<-2,或-1<x<0,或0<x<1,或x>2} |
8.已知f(x)是定义在R上的周期函数,最小正周期为T,则下列函数中恒为周期函数的是( )
| A. | f(x2+x) | B. | f(2x+x) | C. | f(sinx+x) | D. | f(f(x)+x) |
9.不等式m2+1≥2m中等号成立的条件是 ( )
| A. | m=1 | B. | m=±1 | C. | m=-1 | D. | m=0 |
6.下列数列是等比数列的是( )
| A. | 1,1,1,1,… | B. | …0,0,0,0, | C. | 0,12,14,18,… | D. | -1,-1,1,1 |