题目内容
8.已知f(x)是定义在R上的周期函数,最小正周期为T,则下列函数中恒为周期函数的是( )| A. | f(x2+x) | B. | f(2x+x) | C. | f(sinx+x) | D. | f(f(x)+x) |
分析 由已知条件,在所给的四个函数中,分别令x=x+T,利用周期函数的定义进行验证,能求出正确结果.
解答 解:∵f(x)是定义在R上的周期函数,最小正周期为T,
∴在A中:f(x2+x),令x=x+T,得:
f[(x+T)2+(x+T)]=f(x2+x+2Tx+T2+T),
∴f(x2+x)不恒为周期函数;
在B中:f(2x+x),令x=x+T,得:
f(2x+T+x+T)=f(2x•2T+x+T),
∴f(2x+x)不恒为周期函数;
在C中:f(sinx+x),令x=x+T,得:
f(sin(x+T)+x+T),
∴f(sinx+x)不恒为周期函数;
在D中:f(f(x)+x),令x=x+T,得:
f(f(x+T)+x+T)=f(f(x)+x+T),
∴f(f(x)+x)恒为周期函数,其最小正周期为T.
故选:D.
点评 本题考查周期函数的判断,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
13.设f(x)是R上的任意函数,下列叙述正确的是( )
| A. | f(|x|)是奇函数 | B. | |f(x)|是偶函数 | C. | f(x)+f(-x)是奇函数 | D. | f(x)-f(-x)是奇函数 |
17.已知x=$\frac{π}{3}$是函数f(x)=(b-$\sqrt{3}a$)sinx+(a-b)cosx(a≠0)的一个零点,则函数g(x)=asinx-bcosx的图象可能是( )
| A. | 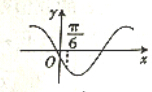 | B. | 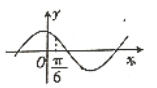 | ||
| C. | 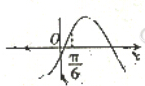 | D. | 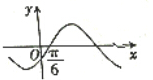 |
18.函数f(x)=ax与g(x)=-x+a的图象大致是( )
| A. | 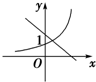 | B. | 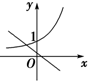 | C. | 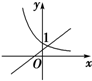 | D. | 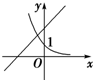 |