题目内容
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)是否存直线 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 .
.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)是否存直线
 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.(1)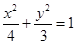 ;(2)
;(2)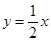 .
.
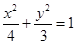 ;(2)
;(2)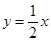 .
.本试题主要考查了椭圆的方程和性质的和运用。第一问中,利用待定系数法求解椭圆的标准方程即可。结合椭圆的离心率为 ,且经过点
,且经过点 可得
可得
(2)中假设存在直线 满足条件,由题意可设直线
满足条件,由题意可设直线 的方程为
的方程为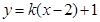 ,联立方程组
,联立方程组
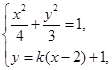 结合韦达定理可知且
结合韦达定理可知且 ,即
,即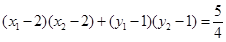 ,
,
所以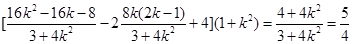 ,解得
,解得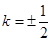 .
.
因为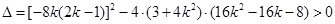 ,解得
,解得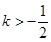 .
.
所以最终得到k=1/2.
解:(Ⅰ)设椭圆 的方程为
的方程为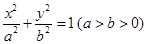 ,由题意得
,由题意得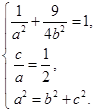
解得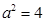 ,
,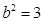 ,故椭圆
,故椭圆 的方程为
的方程为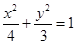 . ……………………5分
. ……………………5分
(Ⅱ)若存在直线 满足条件,由题意可设直线
满足条件,由题意可设直线 的方程为
的方程为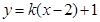 ,
,
由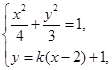 得
得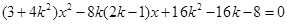 .
.
因为直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为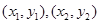 ,
,
所以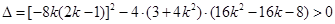 .
.
整理得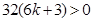 .
.
解得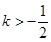 .
.
又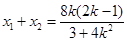 ,
,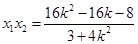 ,
,
且 ,即
,即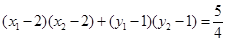 ,
,
所以 . 即
. 即 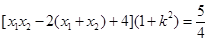 .
.
所以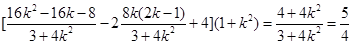 ,解得
,解得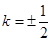 .
.
所以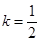 .于是存在直线
.于是存在直线 满足条件,其的方程为
满足条件,其的方程为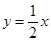 . ………………13分
. ………………13分
 ,且经过点
,且经过点 可得
可得(2)中假设存在直线
 满足条件,由题意可设直线
满足条件,由题意可设直线 的方程为
的方程为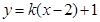 ,联立方程组
,联立方程组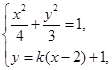 结合韦达定理可知且
结合韦达定理可知且 ,即
,即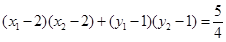 ,
,所以
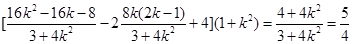 ,解得
,解得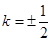 .
.因为
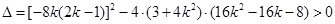 ,解得
,解得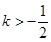 .
.所以最终得到k=1/2.
解:(Ⅰ)设椭圆
 的方程为
的方程为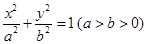 ,由题意得
,由题意得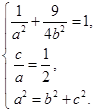
解得
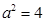 ,
,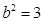 ,故椭圆
,故椭圆 的方程为
的方程为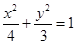 . ……………………5分
. ……………………5分(Ⅱ)若存在直线
 满足条件,由题意可设直线
满足条件,由题意可设直线 的方程为
的方程为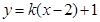 ,
,由
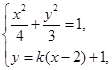 得
得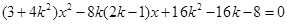 .
.因为直线
 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为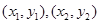 ,
,所以
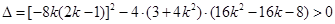 .
.整理得
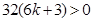 .
.解得
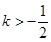 .
.又
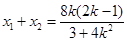 ,
,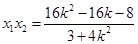 ,
,且
 ,即
,即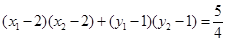 ,
,所以
 . 即
. 即 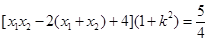 .
.所以
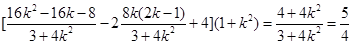 ,解得
,解得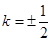 .
.所以
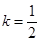 .于是存在直线
.于是存在直线 满足条件,其的方程为
满足条件,其的方程为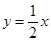 . ………………13分
. ………………13分
练习册系列答案
相关题目
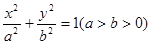 的右焦点为
的右焦点为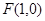 ,
,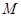 为椭圆的上顶点,
为椭圆的上顶点,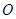 为坐标原点,且△
为坐标原点,且△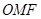 是等腰直角三角形.
是等腰直角三角形.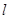 交椭圆于
交椭圆于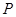 ,
,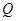 两点, 且使点
两点, 且使点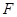 为△
为△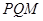 的垂心(垂心:三角形三边高线的交点)?若存在,求出直线
的垂心(垂心:三角形三边高线的交点)?若存在,求出直线 的一个焦点为F(2,0),离心率
的一个焦点为F(2,0),离心率 .
. 与椭圆交于不同的A,B两点,与y轴交于E点,且
与椭圆交于不同的A,B两点,与y轴交于E点,且 ,求实数m的值.
,求实数m的值.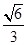 的椭圆
的椭圆
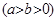 经过点
经过点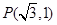 .
.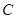 的方程;
的方程; 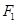 且不与
且不与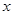 轴垂直的直线
轴垂直的直线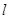 交椭圆
交椭圆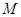 、
、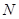 两点,若
两点,若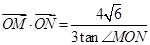 (
(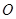 为坐标原点),求直线
为坐标原点),求直线 的离心率
的离心率 ,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足
,点F为椭圆的右焦点,点A、B分别为椭圆的左、右顶点,点M为椭圆的上顶点,且满足 (1)求椭圆C的方程;
(1)求椭圆C的方程; ,当直线
,当直线 的垂心(三角形三条高的交点)?若存在,求出直线
的垂心(三角形三条高的交点)?若存在,求出直线
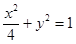 的左焦点为
的左焦点为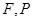 为椭圆上一点,其横坐标为
为椭圆上一点,其横坐标为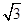 ,则
,则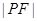 =( )
=( ) 



 是椭圆
是椭圆 的两个焦点,
的两个焦点, 是椭圆上的动点(不能重合于长轴的两端点),
是椭圆上的动点(不能重合于长轴的两端点), 是
是 的内心,直线
的内心,直线 交
交 轴于点
轴于点 ,则
,则
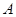 、
、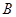 、
、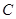 是长轴长为
是长轴长为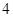 的椭圆上的三点,点
的椭圆上的三点,点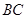 过椭圆中心
过椭圆中心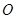 ,且
,且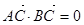 ,
,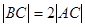 ,
,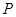 、
、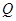 使
使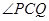 的平分线垂直
的平分线垂直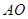 ,则是否存在实数
,则是否存在实数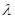 使
使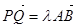 ?请说明理由。
?请说明理由。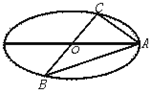
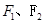 是椭圆
是椭圆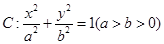 的两个焦点,P为椭圆
的两个焦点,P为椭圆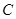 上的一点,且
上的一点,且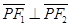 .若
.若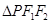 的面积为9,则
的面积为9,则 .
.