题目内容

10．设x1，x2为函数f（x）=x2+（a2-1）x+（a-2）的两个零点，且x1＜1＜x2，则实数a的取值范围是（-2，1）．

分析 函数f（x）=x2+（a2-1）x+（a-2）的两个零点，且x1＜1＜x2，可得f（1）＜0，从而可求实数a的取值范围

解答 解：∵函数f（x）=x2+（a2-1）x+（a-2）的两个零点，且x1＜1＜x2，
函数f（x）=x2+（a2-1）x+（a-2）的两个零点一个大于1，一个小于1，
∴f（1）＜0，
∴12+（a2-1）+（a-2）＜0
∴-2＜a＜1
∴实数a的取值范围是（-2，1）．
故答案为：（-2，1）．

点评 本题考查的重点是函数的零点判定定理，解题的关键是根据题意，建立不等式．

练习册系列答案
相关题目
20．定义在（-1，1）上的函数f（x）满足：对任意x，y∈（-1，1），都有f（x）+f（y）=f（$\frac{x+y}{1+xy}$）．
（1）求证：函数f（x）是奇函数；
（2）若当 x∈（-1，0）时，有f（x）＞0，求证：f（x）在（-1，1）上是减函数；
（3）f（1-a）+f（1-3a）＜0，求实数a的取值范围．
1．如图，正方体ABCD-A1B1C1D1的棱长为1，E，F分别为线段AA1，B1C上的点，求三棱锥D1-EDF的体积．
18．如图，AC1是正方体ABCD-A1B1C1D1的对角线．
（1）求证：平面A1BD∥平面CD1B1；
（2）求证：直线AC1⊥直线BD．
5．已知定义域为R的函数f（x）满足f（1）=3，且f（x）的导数f′（x）＜2x+1，则不等式f（3x）≥9x2+3x+1的解集为（-∞，$\frac{1}{3}$]．
15．已知函数f（x）=Asin（ωx-$\frac{π}{6}$）+1（A＞0，ω＞0）的最大值为3，其图象的相邻两条对称轴之间的距离为$\frac{π}{2}$．
（1）求函数f（x）对称中心的坐标；
（2）求函数f（x）在区间[0，$\frac{π}{2}$]上的值域．
2．若集合A={x|2x+1＞0}，B={x|2x-1＜2}，则A∩B={x|$\frac{1}{2}$＜x＜$\frac{3}{2}$}．
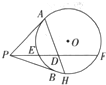19．如图，已知点P是圆O外一点，过P做圆O的切线PA，PB，切点分别为A，B，过P做一条割线交圆O于E，F，若2PA=PF，取PF的中点D，连接AD，并延长交圆于H．
（1）求证：四点O，A，P，B共圆；
（2）求证：PB2=2ED×DF．
20．下列4个命题：
①命题“若x2-x=0，则x=1”的逆否命题为“若x≠1，则x2-x≠0”；
②若“?p或q”是假命题，则“p且?q”是真命题；
③若p：x（x-2）≤0，q：log2x≤1，则p是q的必要不充分条件；
④若命题p：存在x∈R，使得2x＜x2，则?p：任意x∈R，均有2x≥x2；
其中正确命题的个数是（　　）
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网