题目内容
已知正三棱锥P-ABC的主视图和俯视图如图所示，则此三棱锥外接球的表面积为（ ）
A、
| ||
B、
| ||
C、
| ||
| D、12π |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：根据三视图判断正三棱锥的侧面上的高与底面正三角形的边长，借助直观图求出外接球的半径，代入球的表面积公式计算．
解答：
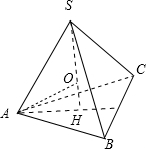解：由正视图与侧视图知，正三棱锥的侧面上的高为
，底面正三角形的边长为2
，如图：
其中SA=4，AH=2，SH=2
，
设其外接球的球心为0，半径为R，则：OS=OA=R，
∴R+
=2
，
∴R=
，
∴外接球的表面积S=4π×
=
．
故选：B．
解：由正视图与侧视图知，正三棱锥的侧面上的高为| 13 |
| 3 |
其中SA=4，AH=2，SH=2
| 3 |
设其外接球的球心为0，半径为R，则：OS=OA=R，
∴R+
| R2-4 |
| 3 |
∴R=
4
| ||
| 3 |
∴外接球的表面积S=4π×
| 16 |
| 3 |
| 64π |
| 3 |
故选：B．
点评：本题考查了由三视图求几何体的外接球的表面积，根据三棱锥的结构特征求出外接球的半径是解答本题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
定积分
（3x2-1）dx的值为（ ）
| ∫ | 2 0 |
| A、0 | B、6 | C、11 | D、12 |
三棱锥D-ABC及其三视图中的主视图和左视图如图所示，则棱BD的长为（ ）
A、4
| ||
| B、4 | ||
C、3
| ||
D、2
|
直线3x+4y-5=0的斜率为k，则k的值为（ ）
A、
| ||
B、
| ||
C、-
| ||
D、-
|
直线y=kx-2与抛物线y2=6x交于A、B两点，且线段AB的中点的纵坐标为3，则k的值是（ ）
| A、1 | B、-2 |
| C、1或-2 | D、以上都不是 |
下列说法正确的是（ ）
| A、命题“?x∈R使得x2+2x+3＜0”的否定是：“?x∈R，x2+2x+3＞0” | ||
| B、“a＞1”是“f（x）=logax（a＞0，a≠1）在（0，+∞）上为增函数”的充要条件 | ||
| C、“p∧q为真命题”是“p∨q为真命题”的必要不充分条件 | ||
D、命题p：“?x∈R，sinx+cosx≤
|