题目内容
13.将函数f(x)=sin2x+$\sqrt{3}$cos2x图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将图象上所有点向右平移$\frac{π}{6}$个单位长度,得到函数g (x)的图象,则g(x)图象的一条对称轴方程是( )| A. | x=一$\frac{π}{6}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{24π}{25}$ | D. | x=$\frac{π}{3}$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,求得g(x)图象的一条对称轴方程.
解答 解:将函数f(x)=sin2x+$\sqrt{3}$cos2x=2($\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x)=2sin(2x+$\frac{π}{3}$)的图象上
所有点的横坐标伸长到原来的2倍(纵坐标不变),可得y=2sin(x+$\frac{π}{3}$)的图象;
再将图象上所有点向右平移$\frac{π}{6}$个单位长度,
得到函数g (x)=2sin(x-$\frac{π}{6}$+$\frac{π}{3}$)=2sin(x+$\frac{π}{6}$)的图象的图象的图象,
令x+$\frac{π}{6}$=kπ+$\frac{π}{2}$,求得x=kπ+$\frac{π}{3}$,k∈Z.
令k=0,可得g(x)图象的一条对称轴方程是x=$\frac{π}{3}$,
故选:D.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.甲、乙、丙、丁、戊5个人排成一排,其中丙必须排在甲、乙之间(不一定相邻),则不同的排法种数为( )
| A. | 80 | B. | 40 | C. | 32 | D. | 16 |
5.当$x∈[-\frac{π}{3},\frac{π}{3}]$时,函数$f(x)=\sqrt{2}sin\frac{x}{4}cos\frac{x}{4}+\sqrt{6}{cos^2}\frac{x}{4}-\frac{{\sqrt{6}}}{2}$的最小值为( )
| A. | $-\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
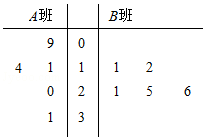 某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).
某校为了了解A,B两班学生寒假期间观看《中国诗词大会》的时长,分别从这两个班中随机抽取5名学生进行调查,将他们观看的时长(单位:小时)作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).