题目内容
12.求下列函数的定义域:(1)y=$\frac{\sqrt{x+1}}{x+2}$;
(2)y=$\frac{\sqrt{2x-1}}{x-1}$+(5x-4)0.
分析 (1)由$\left\{\begin{array}{l}{x+1≥0}\\{x+2≠0}\end{array}\right.$,解得x范围即可得出.
(2)由$\left\{\begin{array}{l}{2x-1≥0}\\{x-1≠0}\\{5x-4≠0}\end{array}\right.$,解得x范围即可得出.
解答 解:(1)由$\left\{\begin{array}{l}{x+1≥0}\\{x+2≠0}\end{array}\right.$,解得x≥-1,∴此函数的定义域为{x|x≥-1}.
(2)由$\left\{\begin{array}{l}{2x-1≥0}\\{x-1≠0}\\{5x-4≠0}\end{array}\right.$,解得x≥$\frac{1}{2}$,x≠1,x$≠\frac{4}{5}$.
∴函数的定义域为{x|x≥$\frac{1}{2}$,x≠1,x$≠\frac{4}{5}$}.
点评 本题考查了函数的定义域、不等式的解法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
2.已知某公司现有职员120人,中级管理人员30人,高级管理人员10人,要从其中抽取32个人进行身体健康检查,如果采用分层抽样的方法,则职员中“中级管理人员“和“高级管理人员”各应该抽取的人数为( )
| A. | 8,2 | B. | 8,3 | C. | 6,3 | D. | 6,2 |
3.已知P是以F1,F2为焦点的椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的一点,若PF1⊥PF2,且|PF1|=2|PF2|,则此椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{5}}{3}$ |
17.在△ABC中,角A,B,C所对的边分别为a,b,c,那么a>b是sinA>sinB的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | C. | 充分且必要 | D. | 无关 |
4.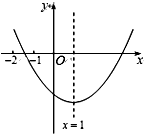 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
①b2-4ac>0;
②abc>0;
③b=-2a;
④9a+3b+c<0,
正确结论的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,在下列结论中:①b2-4ac>0;
②abc>0;
③b=-2a;
④9a+3b+c<0,
正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.为了得到函数y=sin2x-cos2x的图象,可以将函数y=$\sqrt{2}$cos2x的图象( )
| A. | 向左平行移动$\frac{3π}{8}$个单位 | B. | 向右平行移动$\frac{3π}{8}$个单位 | ||
| C. | 向左平行移动$\frac{3π}{4}$个单位 | D. | 向右平行移动$\frac{3π}{4}$个单位 |