Question

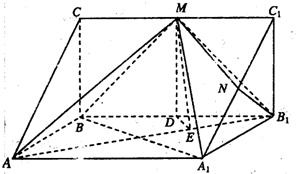
（2010•唐山二模）如图，在直三棱柱ABC-A₁B₁C₁中，∠ABC=90°，AB=BC=2，AA₁=4，M、N分别为CC₁、A₁C₂的中点．
（I）求证：AM⊥平面B₁MN；
（II）求二面角M-AB₁-A₁的大小．

Answer 1

分析：（I）要证明AM⊥平面B₁MN，只需证明AM垂直平面B₁MN内两条相交直线即可，利用平面A₁B₁C₁⊥平面A₁ACC₁证明AM⊥B₁N．
再利用勾股定理证明AM⊥MN，而B₁N，MN为平面B₁MN内两条相交直线，所以可证AM⊥平面B₁MN．
（II）要求二面角M-AB₁-A₁的大小，只需求其平面角的大小，先利用三垂线法找二面角M-AB₁-A₁的平面角，再放入直角三角形中，解三角形即可．

解答：解：（I）∵ABC-A₁B₁C₁是直三棱柱，∴平面A₁B₁C₁⊥平面A₁ACC₁；
∵AB=BC，进而A₁B₁=B₁C₁，
N为A₁C₁的中点，
∴B₁N⊥平面A₁ACC₁，
∵AM?平面A₁ACC₁，
∴B₁N⊥AM，即AM⊥B₁N．
在侧面A₁ACC₁中，C₁M=CM=2，
C₁N=

2

，AC=2

2

，∴Rt△MC₁N∽Rt△ACM，
∴∠C₁MN+∠CMA=90°，
∴AM⊥MN．
∵B₁N∩MN=N，∴AM⊥平面B₁MN．  
（II）取BB₁的中点为D，连接MD，则MD⊥平面A₁AB₁，作DE⊥AB₁，垂足为E，连接ME，则ME⊥AB₁，∠MED为二面角M-AB₁-A₁的补角．
在Rt△ABB1中，DE=

1

2

•

AB•BB1

AB1

=

2

5

，
∴tan∠MED=

MD

DE

=

5

，
∠MED=arctan

5

，…（11分）
故二面角M-AB₁-A₁的大小为π-arctan

5

．

点评：本题考查了线面垂直的判定，以及二面角的求法，属于立体几何中的常规题，应当掌握．