题目内容
如图所示,在直四棱柱ABCDA1B1C1D1中,底面是正方形,E,F,G分别是棱B1B,D1D,DA的中点.求证:平面AD1E∥平面BGF.
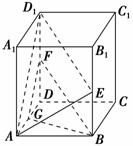
【证明】∵E,F分别是B1B和D1D的中点,
∴D1F//BE,D1F=BE
∴四边形BED1F是平行四边形,∴D1E∥BF.
又∵D1E⊄平面BGF,BF⊂平面BGF,∴D1E∥平面BGF.
∵FG是△DAD1的中位线,∴FG∥AD1.
又AD1⊄平面BGF,FG⊂平面BGF,∴AD1∥平面BGF.
又∵AD1∩D1E=D1,∴平面AD1E∥平面BGF.

练习册系列答案
相关题目
 B.
B. C.
C. D.
D.
 2) 求异面直线PD与BC所成角的大小
2) 求异面直线PD与BC所成角的大小 和
和 ,则( )
,则( ) ,使得
,使得 B.必定存在平面
B.必定存在平面 ,
, ,使得
,使得 ,
,
 、
、 、
、 ,则长方体的对角线长
,则长方体的对角线长 ,长方体的表面积为
,长方体的表面积为 ,长方体的体积为
,长方体的体积为
 中,
中,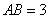 ,
,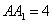 ,
, 为
为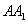 的中点,
的中点,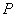 是
是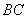 上一点,且由
上一点,且由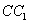 到点
到点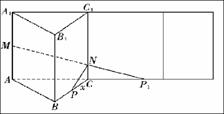
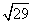 ,设这条最短路线与
,设这条最短路线与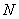 ,求:
,求:  和
和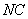 的长.
的长. B.
B.
 D.
D.

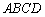 为正方形,
为正方形,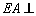 平面
平面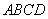 ,
, ,
,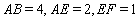 ,
,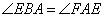
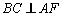 ;
;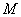 在线段
在线段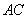 上,且满足
上,且满足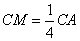 , 求证:
, 求证: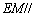 平面
平面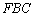 ;
;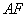 与平面
与平面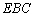 是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
是否垂直?若垂直,请给出证明;若不垂直,请说明理由.