题目内容
已知函数f(x)=x(x-a)2+b在x=2处有极大值.
(Ⅰ)当[-2,4]时,函数y=f(x)的图象在抛物线y=1+45x-9x2的下方,求b的取值范围.
(Ⅱ)若过原点有三条直线与曲线y=f(x)相切,求b的取值范围.
(Ⅰ)当[-2,4]时,函数y=f(x)的图象在抛物线y=1+45x-9x2的下方,求b的取值范围.
(Ⅱ)若过原点有三条直线与曲线y=f(x)相切,求b的取值范围.
考点:利用导数研究函数的极值
专题:函数的性质及应用,导数的概念及应用
分析:(1)其中一个函数的图象在另一个函数图象的下方,转化为两个函数的“差函数”在相应区间内恒小于0的问题;
(2)求切线主要还是抓住切点,因此既然有三条切线,因此应该有三个切点,也就是利用切点表示的方程将原点代入后,得到关于切点横坐标x的方程有三个不同的实数根.再结合导数研究函数的图象求解.
(2)求切线主要还是抓住切点,因此既然有三条切线,因此应该有三个切点,也就是利用切点表示的方程将原点代入后,得到关于切点横坐标x的方程有三个不同的实数根.再结合导数研究函数的图象求解.
解答:
解:(Ⅰ)f(x)=x(x-a)2+b=x3-2ax2+a2x+b⇒f'(x)=3x2-4ax+a2,f'(2)=12-8a+a2=0⇒a=2或a=6,
当a=2时,函数在x=2处取得极小值,舍去;
当a=6时,f'(x)=3x2-24x+36=3(x-2)(x-6),
函数在x=2处取得极大值,符合题意,∴a=6.
∵当x∈[-2,4]时,函数y=f(x)的图象在抛物线y=1+45x-9x2的下方,
∴x3-12x2+36x+b<1+45x-9x2在x∈[-2,4]时恒成立,
即b<-x3+3x2+9x+1在x∈[-2,4]时恒成立,令h(x)=-x3+3x2+9x+1,
则h'(x)=-3x2+6x+9=-3(x-3)(x+1),由h'(x)=0得,x1=-1,x2=3.
∵h(-2)=3,h(-1)=-4,h(3)=28,h(4)=21,
∴h(x)在[-2,4]上的最小值是-4,b<-4.
(Ⅱ)f(x)=x3-12x2+36x+b,设切点为(x0,
-12
+36x0+b),
则切线斜率为f′(x)=3
-24x0+36,
切线方程为y-
+12
-36x0-b=(3
-24x0+36)(x-x0),
即 y=(3
-24x0+36)x-2
+12
+b,
∴-2
+12
+b=0⇒b=2
-12
.
令g(x)=2x3-12x2,则g'(x)=6x2-24x=6x(x-4),
由g'(x)=0得,x1=0,x2=4.
函数g(x)的单调性如下:
∴当-64<b<0时,方程b=g(x)有三个不同的解,过原点有三条直线与曲线y=f(x)相切.
当a=2时,函数在x=2处取得极小值,舍去;
当a=6时,f'(x)=3x2-24x+36=3(x-2)(x-6),
函数在x=2处取得极大值,符合题意,∴a=6.
∵当x∈[-2,4]时,函数y=f(x)的图象在抛物线y=1+45x-9x2的下方,
∴x3-12x2+36x+b<1+45x-9x2在x∈[-2,4]时恒成立,
即b<-x3+3x2+9x+1在x∈[-2,4]时恒成立,令h(x)=-x3+3x2+9x+1,
则h'(x)=-3x2+6x+9=-3(x-3)(x+1),由h'(x)=0得,x1=-1,x2=3.
∵h(-2)=3,h(-1)=-4,h(3)=28,h(4)=21,
∴h(x)在[-2,4]上的最小值是-4,b<-4.
(Ⅱ)f(x)=x3-12x2+36x+b,设切点为(x0,
| x | 3 0 |
| x | 2 0 |
则切线斜率为f′(x)=3
| x | 2 0 |
切线方程为y-
| x | 3 0 |
| x | 2 0 |
| x | 2 0 |
即 y=(3
| x | 2 0 |
| x | 3 0 |
| x | 2 0 |
∴-2
| x | 3 0 |
| x | 2 0 |
| x | 3 0 |
| x | 2 0 |
令g(x)=2x3-12x2,则g'(x)=6x2-24x=6x(x-4),
由g'(x)=0得,x1=0,x2=4.
函数g(x)的单调性如下:
| x | (-∞,0) | 0 | (0,4) | 4 | (4,+∞) |
| g'(x) | + | 0 | - | 0 | + |
| g(x) | ↗ | 极大值0 | ↘ | 极小值-64 | ↗ |
点评:本题充分体现了数形结合的思想在研究函数的零点中的作用,当然利用导数研究单调性、极值之必须走的常规路子.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知A={x∈z|2x2+x-1=0}、B={x|4x2+1=0}.则A∪B=( )
A、{-
| ||||
B、{
| ||||
| C、{-1} | ||||
D、{
|
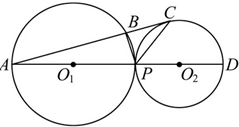 如图,⊙O1和⊙O2外切于点P,延长PO1交⊙O1于点A,延长PO2交⊙O2于点D,若AC与⊙O2相切于点C,且交⊙O1于点B.求证:
如图,⊙O1和⊙O2外切于点P,延长PO1交⊙O1于点A,延长PO2交⊙O2于点D,若AC与⊙O2相切于点C,且交⊙O1于点B.求证: