题目内容
15.设S为实数集R的非空子集.若对任意x,y∈S,都有x+y,x-y,xy∈S,则称S为封闭集,下列说法:①集合S={a+b$\sqrt{3}$|a,b为整数}为封闭集;
②若S为封闭集,则一定有0∈S;
③封闭集一定有无数多个元素;
④若S为封闭集,则满足S⊆T⊆R的任意集合T也是封闭集.
其中的正确的说法是①②(写出所有正确说法的序号).
分析 由题意直接验证①即可判断正误;令x=y可推出②是正确的;找出反例集合S={0},即可判断③的错误;令S={0},T={0,1},推出-1不属于T,判断④是错误的
解答 解:①设x=a+b$\sqrt{3}$,y=c+d$\sqrt{3}$,(a,b,c,d为整数),
则x+y∈S,x-y∈S,xy=(ac+3bd)+(bc+ad)$\sqrt{3}$∈S,S为封闭集,①正确;
②当S为封闭集时,因为x-y∈S,取x=y,得0∈S,②正确;
③对于集合S={0},显然满足所有条件,但S是有限集,③错误;
④取S={0},T={0,1},满足S⊆T⊆C,但由于0-1=-1不属于T,故T不是封闭集,④错误.
故答案为:①②.
点评 本题考查对封闭集定义的理解及运用,考查集合的子集,集合的包含关系判断及应用,以及验证和举反例的方法的应用,是一道中档题

练习册系列答案
相关题目
5.某单位有老年人30 人,中年人60人,青年人90人,为了调查他们的身体状况的某项指标,需从他们中间抽取一个容量为36样本,则老年人、中年人、青年人分别各抽取的人数是( )
| A. | 6,12,18 | B. | 7,11,19 | C. | 6,13,17 | D. | 7,12,17 |
5.已知集合A={x|x2-1=0},则下列式子表示正确的有( )
①1∈A②{1}∈A③∅⊆A④{1,-1}⊆A.
①1∈A②{1}∈A③∅⊆A④{1,-1}⊆A.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
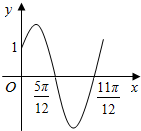 已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<$\frac{π}{2}$)的部分图象如图所示.