题目内容
已知函数 .
.
(Ⅰ)求函数 最大值和最小正周期;
最大值和最小正周期;
(Ⅱ)设 的内角
的内角 的对边分别为
的对边分别为 ,且
,且 ,若
,若 ,求
,求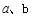 的值
的值
(Ⅰ) 的最大值为0,最小正周期是
的最大值为0,最小正周期是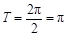 ;(Ⅱ)
;(Ⅱ)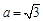 ,
,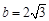 .
.
解析试题分析:(Ⅰ)先化简 ,再求函数
,再求函数 最大值和最小正周期;(Ⅱ)根据正弦定理化简
最大值和最小正周期;(Ⅱ)根据正弦定理化简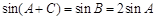 ,由余弦定理得
,由余弦定理得 ,通过解方程求解答案.
,通过解方程求解答案.
试题解析:
(Ⅰ) , (3分)
, (3分)
则 的最大值为0,最小正周期是
的最大值为0,最小正周期是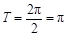 . (5分)
. (5分)
(Ⅱ)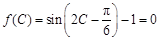 ,则
,则 . (6分)
. (6分)
∵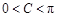 ,∴
,∴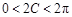 ,∴
,∴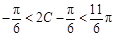 ,
,
∴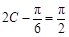 ,∴
,∴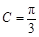 . (7分)
. (7分)
又∵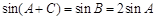 ,由正弦定理得
,由正弦定理得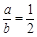 ,① (9分)
,① (9分)
由余弦定理得 ,即
,即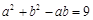 ,② (10分)
,② (10分)
由①②解得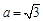 ,
,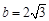 . (12分)
. (12分)
考点:三角变换、正弦定理、余弦定理

练习册系列答案
相关题目
 的三个内角A,B,C的对边,
的三个内角A,B,C的对边,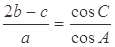
 时,求
时,求 的取值范围.
的取值范围. 

 ,
,
 时,求函数
时,求函数 的值域;
的值域;
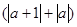 ,当
,当 时恒成立,求
时恒成立,求 的取值范围.
的取值范围. ,
, ,且
,且 ,其中A、B、C是
,其中A、B、C是 ABC的内角,
ABC的内角, 分别是角A,B,C的对边。
分别是角A,B,C的对边。 的取值范围;
的取值范围;
 最小正周期及单调递增区间;
最小正周期及单调递增区间; 时,求
时,求 ,
, ,设函数
,设函数 .
.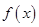 的解析式,并求
的解析式,并求 上的最小值;
上的最小值; 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若 ,
, ,
, ,求
,求 .
. ,
,
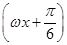 (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.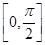 ,f
,f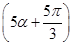 =-
=-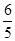 ,f
,f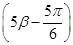 =
=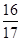 ,求cos(α+β)的值.
,求cos(α+β)的值. 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,
, ,且
,且
 与
与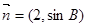 共线,求
共线,求