题目内容
 如图,△ABC为正三角形,边长为a,MN⊥BC,边写出MN与△ABC相交左侧部分的面积y关于AN长度x的解析式(N点异于A、B)
如图,△ABC为正三角形,边长为a,MN⊥BC,边写出MN与△ABC相交左侧部分的面积y关于AN长度x的解析式(N点异于A、B)分析:当0<x≤
时,在直线MN的左侧部分是直角三角形,面积可直接计算出;当
<x<a时,直线MN左侧部分是一个不规则的四边形,直接计算不好算,不如用△ABC的面积减去△BMN的面积来计算较简单.
| a |
| 2 |
| a |
| 2 |
解答:解:当0<x≤
时,在直角△ANM中,AN=x,MN=xtan60°=
x,
∴S△ANM=
x×
x=
x2,即y=
x2;
当
<x<a时,MN与△ABC相交左侧部分的面积y=S△ABC-S△BMN=
a2-
(a-x)2=-
x2+
ax-
a2.
综上可知:y=
| a |
| 2 |
| 3 |
∴S△ANM=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 2 |
当
| a |
| 2 |
| ||
| 4 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| ||
| 4 |
综上可知:y=
|
点评:本题考查三角形的面积计算及分段函数,熟悉面积计算和恰当分段是解决问题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
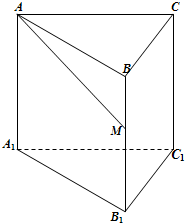 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.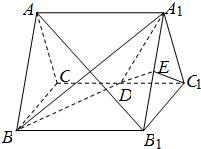 如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点.
如图,已知正三棱柱ABC-A1B1C1的所有棱长都是2,D、E分别为CC1、A1B1的中点. 如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点.
如图,已知正三棱柱ABC-A1B1C1的各条棱长都为a,P为A1B上的点. 如图,已知正三棱柱ABC-A1B1C1的底面边长为
如图,已知正三棱柱ABC-A1B1C1的底面边长为 (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.