题目内容
巳知椭圆G的中心在坐标原点,长轴在x1•x3•x5•…•x2n-1<
<
sin
轴上,离心率为
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为
+
=1
+
=1.
|
| 2 |
| xn |
| yn |
| ||
| 2 |
| x2 |
| 36 |
| y2 |
| 9 |
| x2 |
| 36 |
| y2 |
| 9 |
分析:根据椭圆的定义,可知2a=12,再根据离心率为求出b,就可求出椭圆的方程.
解答:解:且G上一点到G的两个焦点的距离之和为12,根据椭圆的定义,可知2a=12,a=6,又e=
=
,∴c=3
b2=a2-c2=36-27=9,
∴椭圆的方程为
+
=1
故答案为:
+
=1.
| c |
| a |
| ||
| 2 |
| 3 |
∴椭圆的方程为
| x2 |
| 36 |
| y2 |
| 9 |
故答案为:
| x2 |
| 36 |
| y2 |
| 9 |
点评:本题考查椭圆的定义,标准方程、几何性质,属于基础题.

练习册系列答案
相关题目
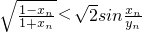 轴上,离心率为
轴上,离心率为 ,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为________.
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为________.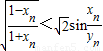 轴上,离心率为
轴上,离心率为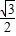 ,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______.
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为______.