题目内容
p：ax2+by2=c为双曲线，q：ab＜0，则p是q的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、既不充分也不必要条件 |
| D、充要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：p：ax2+by2=c为双曲线，化为
+
=1，可得
•
＜0，于是ab＜0，c≠0．即可判断出．
| x2 | ||
|
| y2 | ||
|
| c |
| a |
| c |
| b |
解答：
解：p：ax2+by2=c为双曲线，化为
+
=1，则
•
＜0，∴ab＜0，c≠0．
因此p是q的既不必要不充分条件．
故选：C．
| x2 | ||
|
| y2 | ||
|
| c |
| a |
| c |
| b |
因此p是q的既不必要不充分条件．
故选：C．
点评：本题考查了双曲线的标准方程、充分必要的判定，属于基础题．
练习册系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
| ∫ | 0 -π |
| A、1-e-π |
| B、1+e-π |
| C、-e-π |
| D、πe-π-1 |
已知正三棱柱ABC-A′B′C′（底面为正三角形，侧棱垂直于底面）的正视图和侧视图如图所示．设△ABC、△A′B′C′的中心为O，O′，现将此三棱柱绕直线OO′旋转．射线OA旋转所成的角为x弧度（x可取任一实数，逆时针为正角，顺时针为负角）．对应的俯视图的面积为S（x），则S（x）的最小正周期和值域分别为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知集合A={1，-2，-3，4}，B={x|x=|n|，n∈A}，则A∩B=（ ）
| A、{1，-2} |
| B、{-2，-3} |
| C、{2，3} |
| D、{1，4} |
（文科）双曲线x2-y2=1的焦点坐标为（ ）
| A、（±1，0） | ||
| B、（0，±1） | ||
C、（±
| ||
D、（0，±
|
已知x，y∈R，若p：x＜1且y＜1，q：x+y≥2．则p是￢q的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知sin
+cos
=
，则cos2θ=（ ）
| θ |
| 2 |
| θ |
| 2 |
| 1 |
| 2 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
在如图所示的程序框图中输入n=3，结果会输出（ ）
| A、2 | B、4 | C、6 | D、8 |
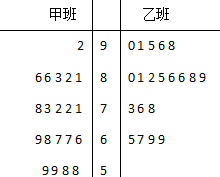我市某校某数学老师这学期分别用m，n两种不同的教学方式试验高一甲、乙两个班（人数均为60人，入学数学平均分和优秀率都相同，勤奋程度和自觉性都一样）．现随机抽取甲、乙两班各20名的数学期末考试成绩，并作出茎叶图如图所示．