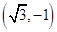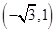题目内容
在极坐标系中，圆C的方程为
＝2
sin（θ＋
），以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为
（t为参数）．
（Ⅰ）求直线l和圆C的直角坐标方程；
（Ⅱ）判断直线l和圆C的位置关系．
＝2sin（θ＋），以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为（t为参数）．（Ⅰ）求直线l和圆C的直角坐标方程；
（Ⅱ）判断直线l和圆C的位置关系．
（Ⅰ）
.（Ⅱ）所以直线
和圆
相交．
.（Ⅱ）所以直线和圆相交．(I)根据
,对圆C的方程两边同乘以,再转化成普通方程即可.直线l的方程通过消去参数t,转化为直角坐标方.
(II)通过圆心到直线的距离与半径进行比较确定直线与圆的位置关系
（Ⅰ）消去参数
，得直线的直角坐标方程为
.………………… 2分
由
，即
，两边同乘以
得
，得⊙的直角坐标方程为：. …… 6分
（Ⅱ）圆心到直线的距离
，…… 8分因为 
，… 9分
所以直线和圆相交．
,对圆C的方程两边同乘以,再转化成普通方程即可.直线l的方程通过消去参数t,转化为直角坐标方.(II)通过圆心到直线的距离与半径进行比较确定直线与圆的位置关系
（Ⅰ）消去参数
，得直线的直角坐标方程为.………………… 2分由
，即，两边同乘以得，得⊙的直角坐标方程为：. …… 6分（Ⅱ）圆心
到直线的距离，…… 8分因为 ，… 9分所以直线
和圆相交．
练习册系列答案
优生乐园系列答案
相关题目
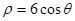，曲线C2的极坐标方程为
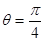，曲线C1，C2相交于A，B两点
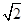为半径的圆在以直角坐标系的原点为极点，以ox为极轴的极坐标系中对应的极坐标方程为（ ）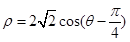
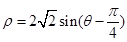
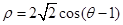
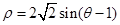
它与曲线C：
交于A、B两点。
，求点P到线段AB中点M的距离。
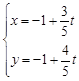（为参数），曲线
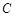的极坐标方程为
．
，
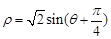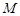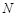两点，求
：
，求圆心
的距离为 
的一条切线的是（ ） 
中，曲线
的交点的极坐标为 。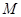
的极坐标是
，则点
