题目内容
12.已知三个复数z1,z2,z3,并且|z1|=|z2|=|z3|=1,z1,z2所对应的向量$\overrightarrow{o{z}_{1}}$,$\overrightarrow{o{z}_{2}}$满足$\overrightarrow{o{z}_{1}}$•$\overrightarrow{o{z}_{2}}$=0,则|z1+z2-z3|的取值范围是[$\sqrt{2}-1$,$\sqrt{2}+1$].分析 由题意画出图形,再由|z1+z2-z3|的几何意义求解.
解答 解:由题意可知:复数z1,z2,z3对应的点Z1,Z2,Z3在单位圆上,
又$\overrightarrow{O{Z}_{1}}•\overrightarrow{O{Z}_{2}}=0$,∴OZ1⊥OZ2.
不妨设Z1(1,0),Z2(0,1),如图: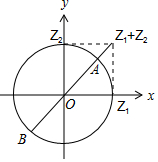
∴当Z3与A重合时,|z1+z2-z3|有最小值为$\sqrt{2}-1$;
当Z3与B重合时,|z1+z2-z3|有最大值为$\sqrt{2}+1$.
∴|z1+z2-z3|的取值范围是[$\sqrt{2}-1$,$\sqrt{2}+1$].
故答案为:[$\sqrt{2}-1$,$\sqrt{2}+1$].
点评 本题考查复数模的求法,考查向量垂直与数量积的关系,是中档题.

练习册系列答案
相关题目
2.从一批含有11只正品,2只次品的产品中,不放回地抽取3次,每次抽取1只,设抽得次品数为X,则E(5X+1)的值为( )
| A. | $\frac{42}{13}$ | B. | $\frac{12}{13}$ | C. | $\frac{41}{11}$ | D. | $\frac{6}{13}$ |
7.抛物线的顶点在原点,焦点是椭圆4x2+y2=1的一个焦点,则此抛物线的焦点到准线的距离是( )
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{1}{2}\sqrt{3}$ | D. | $\frac{1}{4}\sqrt{3}$ |
7.按如图的规律所拼成的一图案共有1024个大小相同的小正三角形“△”或“?”,则该图案共有( )


| A. | 16层 | B. | 32层 | C. | 64层 | D. | 128层 |