题目内容
【题目】如图所示的几何体中,四边形![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,且
,且![]() ,
,![]() .
.
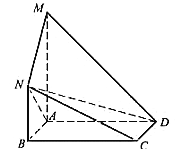
(1)求证: ![]() 面
面![]() ;
;
(2)求棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]() .
.
【解析】分析:(1) 取![]() 中点
中点![]() ,根据平几知识得四边形
,根据平几知识得四边形![]() 为矩形,即得
为矩形,即得![]() ,再根据线面平行判定定理得结论, (2)先证AD垂直平面ABNM,再根据等体积法以及锥体体积公式得结果.
,再根据线面平行判定定理得结论, (2)先证AD垂直平面ABNM,再根据等体积法以及锥体体积公式得结果.
详解:
(1) ![]() 平面
平面![]() ,取
,取![]() 中点
中点![]() ,
,
连接![]()
![]() 平面
平面![]() ,
,![]() ,
,
四边形![]() 为矩形
为矩形
![]() 平面
平面![]() ,
,![]()
![]() ,
,![]()
![]() 四边形
四边形![]() 为平行四边形
为平行四边形
![]()
![]() 平面
平面![]()
![]() 平面
平面![]()
(2)以平面![]() 为底,
为底,![]() 为高
为高
![]() ,
,![]()
![]()
点睛:空间几何体体积问题的常见类型及解题策略
(1)若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.
(2)若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
