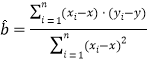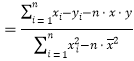题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)证明:![]() 只有一个零点.
只有一个零点.
【答案】解:
(1)当a=3时,f(x)=![]() ,f ′(x)=
,f ′(x)=![]() .
.
令f ′(x)=0解得x=![]() 或x=
或x=![]() .
.
当x∈(–∞,![]() )∪(
)∪(![]() ,+∞)时,f ′(x)>0;
,+∞)时,f ′(x)>0;
当x∈(![]() ,
,![]() )时,f ′(x)<0.
)时,f ′(x)<0.
故f(x)在(–∞,![]() ),(
),(![]() ,+∞)单调递增,在(
,+∞)单调递增,在(![]() ,
,![]() )单调递减.
)单调递减.
(2)由于![]() ,所以
,所以![]() 等价于
等价于![]() .
.
设![]() =
=![]() ,则g ′(x)=
,则g ′(x)=![]() ≥0,仅当x=0时g ′(x)=0,所以g(x)在(–∞,+∞)单调递增.故g(x)至多有一个零点,从而f(x)至多有一个零点.
≥0,仅当x=0时g ′(x)=0,所以g(x)在(–∞,+∞)单调递增.故g(x)至多有一个零点,从而f(x)至多有一个零点.
又f(3a–1)=![]() ,f(3a+1)=
,f(3a+1)=![]() ,故f(x)有一个零点.
,故f(x)有一个零点.
综上,f(x)只有一个零点.
【解析】分析:(1)将![]() 代入,求导得
代入,求导得![]() ,令
,令![]() 求得增区间,令
求得增区间,令![]() 求得减区间;(2)令
求得减区间;(2)令![]() ,即
,即![]() ,则将问题转化为函数
,则将问题转化为函数![]() 只有一个零点问题,研究函数
只有一个零点问题,研究函数![]() 单调性可得.
单调性可得.
详解:(1)当a=3时,f(x)=![]() ,f ′(x)=
,f ′(x)=![]() .
.
令f ′(x)=0解得x=![]() 或x=
或x=![]() .
.
当x∈(–∞,![]() )∪(
)∪(![]() ,+∞)时,f ′(x)>0;
,+∞)时,f ′(x)>0;
当x∈(![]() ,
,![]() )时,f ′(x)<0.
)时,f ′(x)<0.
故f(x)在(–∞,![]() ),(
),(![]() ,+∞)单调递增,在(
,+∞)单调递增,在(![]() ,
,![]() )单调递减.
)单调递减.
(2)由于![]() ,所以
,所以![]() 等价于
等价于![]() .
.
设![]() =
=![]() ,则g ′(x)=
,则g ′(x)=![]() ≥0,仅当x=0时g ′(x)=0,所以g(x)在(–∞,+∞)单调递增.故g(x)至多有一个零点,从而f(x)至多有一个零点.
≥0,仅当x=0时g ′(x)=0,所以g(x)在(–∞,+∞)单调递增.故g(x)至多有一个零点,从而f(x)至多有一个零点.
又f(3a–1)=![]() ,f(3a+1)=
,f(3a+1)=![]() ,故f(x)有一个零点.
,故f(x)有一个零点.
综上,f(x)只有一个零点.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】(本小题满分12分)
2018年2月22日上午,山东省省委、省政府在济南召开山东省全面展开新旧动能转换重大工程动员大会,会议动员各方力量,迅速全面展开新旧动能转换重大工程.某企业响应号召,对现有设备进行改造,为了分析设备改造前后的效果,现从设备改造前后生产的大量产品中各抽取了200件产品作为样本,检测一项质量指标值,若该项质量指标值落在![]() 内的产品视为合格品,否则为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.
内的产品视为合格品,否则为不合格品.图1是设备改造前的样本的频率分布直方图,表1是设备改造后的样本的频数分布表.

表1:设备改造后样本的频数分布表
质量指标值 |
|
|
|
|
|
|
频数 | 4 | 36 | 96 | 28 | 32 | 4 |
(1)完成下面的![]() 列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
列联表,并判断是否有99%的把握认为该企业生产的这种产品的质量指标值与设备改造有关;
设备改造前 | 设备改造后 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
(2)根据图1和表1提供的数据,试从产品合格率的角度对改造前后设备的优劣进行比较;
(3)根据市场调查,设备改造后,每生产一件合格品企业可获利180元,一件不合格品亏损 100元,用频率估计概率,则生产1000件产品企业大约能获利多少元?
附:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 .
.
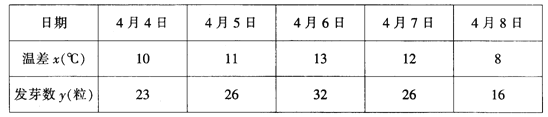
【题目】某互联网公司为了确定下一季度的前期广告投入计划,收集了近![]() 个月广告投入量
个月广告投入量![]() (单位:万元)和收益
(单位:万元)和收益![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
月份 |
|
|
|
|
|
|
广告投入量 |
|
|
|
|
|
|
收益 |
|
|
|
|
|
|
他们分别用两种模型①![]() ,②
,②![]() 分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
分别进行拟合,得到相应的回归方程并进行残差分析,得到如图所示的残差图及一些统计量的值:
|
|
|
|
|
|
|
|

(Ⅰ)根据残差图,比较模型①,②的拟合效果,应选择哪个模型?并说明理由;
(Ⅱ)残差绝对值大于![]() 的数据被认为是异常数据,需要剔除:
的数据被认为是异常数据,需要剔除:
(ⅰ)剔除异常数据后求出(Ⅰ)中所选模型的回归方程
(ⅱ)若广告投入量![]() 时,该模型收益的预报值是多少?
时,该模型收益的预报值是多少?
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
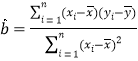
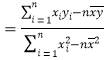 ,
,![]() .
.