题目内容
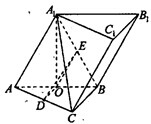
 如图,在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°,D、E分别是AC、A1B的中点.
如图,在斜三棱柱ABC-A1B1C1中,四边形ABB1A1是菱形,四边形CBB1C1是矩形,AB⊥BC,CB=3,AB=4,∠A1AB=60°,D、E分别是AC、A1B的中点.(Ⅰ)求证:平面CA1B⊥平面ABB1A1;
(Ⅱ)求证:DE∥平面CBB1C1;
(Ⅲ)求四面体A1ABC的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)由已知中四边形BCC1B1是矩形,AB⊥BC,我们易由线面垂直的判定定理得到CB⊥平面ABB1A1,再由面面垂直的判定定理,即可得到平面CA1B⊥平面ABB1A1;
(Ⅱ)证明平面DEO∥平面CBB1C1,可得DE∥平面CBB1C1;
(Ⅲ)证明A1O⊥平面ABC,可求四面体A1ABC的体积.
(Ⅱ)证明平面DEO∥平面CBB1C1,可得DE∥平面CBB1C1;
(Ⅲ)证明A1O⊥平面ABC,可求四面体A1ABC的体积.
解答:
 (Ⅰ证明:∵四边形BCC1B1是矩形,AB⊥BC
(Ⅰ证明:∵四边形BCC1B1是矩形,AB⊥BC
∴AB⊥BC,BC⊥BB1,AB∩BB1=B
∴CB⊥平面ABB1A1,
∵CB?平面CA1B
∴平面CA1B⊥平面ABB1A1;
(Ⅱ)证明:取AB的中点O,连接OD,OE,则
∵D、E分别是AC、A1B的中点,
∴OD∥BC,OE∥AA1∥BB1,
∵OD∩OE=O,BC∩BB1=B,
∴平面DEO∥平面CBB1C1,
∵DE?平面DEO,
∴DE∥平面CBB1C1;
(Ⅲ)连接A1O,则
∵四边形ABB1A1是菱形,∠A1AB=60°,
∴A1O⊥AB,
∵BC⊥平面ABB1A1,
∴BC⊥A1O,
∵AB∩BC=B,
∴A1O⊥平面ABC,
∴VA1ABC=
×(
×3×4)×2
=4
.
 (Ⅰ证明:∵四边形BCC1B1是矩形,AB⊥BC
(Ⅰ证明:∵四边形BCC1B1是矩形,AB⊥BC∴AB⊥BC,BC⊥BB1,AB∩BB1=B
∴CB⊥平面ABB1A1,
∵CB?平面CA1B
∴平面CA1B⊥平面ABB1A1;
(Ⅱ)证明:取AB的中点O,连接OD,OE,则
∵D、E分别是AC、A1B的中点,
∴OD∥BC,OE∥AA1∥BB1,
∵OD∩OE=O,BC∩BB1=B,
∴平面DEO∥平面CBB1C1,
∵DE?平面DEO,
∴DE∥平面CBB1C1;
(Ⅲ)连接A1O,则
∵四边形ABB1A1是菱形,∠A1AB=60°,
∴A1O⊥AB,
∵BC⊥平面ABB1A1,
∴BC⊥A1O,
∵AB∩BC=B,
∴A1O⊥平面ABC,
∴VA1ABC=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面平行的判定,其中等体积法,是转化思想在解答点到平面距离问题中最常用的方法.

练习册系列答案
相关题目
把曲线C1:
(θ为参数)上各点的横坐标压缩为原来的
,纵坐标压缩为原来的
,得到的曲线C2为( )
|
| 1 |
| 4 |
| ||
| 4 |
| A、12x2+4y2=1 | ||
B、4x2+
| ||
C、x2+
| ||
| D、3x2+4y2=4 |
 如图所示,江边有一座高为30m的瞭望塔AB,江中有两条船C、D,由塔顶A测得两船C、D的俯角分别为45°和30°,而且两条船C、D与塔底部B连线所成的∠CBD大小为30°,求两条船C、D间的距离为多少米?
如图所示,江边有一座高为30m的瞭望塔AB,江中有两条船C、D,由塔顶A测得两船C、D的俯角分别为45°和30°,而且两条船C、D与塔底部B连线所成的∠CBD大小为30°,求两条船C、D间的距离为多少米?