Question

设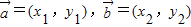，定义一种运算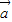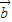：⊕=（x₁x₂，y₁y₂）．已知，，．
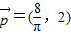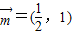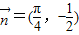（1）证明：（⊕）⊥；
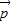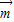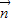（2）点P（x，y）在函数g（x）=sinx的图象上运动，点Q（x，y）在函数y=f（x）的图象上运动，且满足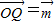⊕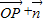（其中O为坐标原点），求函数f（x）的单调递减区间．

Answer 1

【答案】分析：（1）根据该运算的定义，先求出⊕，然后只需证明（⊕）•=0即可；
（2）由⊕可得x和x的方程组，消掉x可得f（x），利用余弦函数的单调性可求得答案；
解答：解：（1），，依题意得⊕=，
又，∴（⊕）•=+2×（）=0，
∴（⊕）⊥；
（2），，由足⊕，得
，即，
消去x，得，即，
令2kπ-π≤2x≤2kπ（k∈Z），得，
∴函数的单调递减区间是[，kπ]（k∈Z）．
点评：本题考查三角恒等变换、复合函数的单调性，考查学生对问题的理解应用能力．