题目内容
已知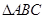 中,角
中,角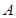 、
、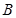 、
、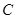 的对边分别为
的对边分别为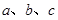 ,且
,且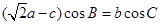 .
.
(1)求角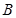 的大小;
的大小;
(2)设向量 ,且
,且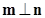 ,求
,求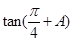 的值.
的值.
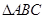 中,角
中,角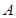 、
、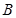 、
、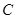 的对边分别为
的对边分别为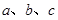 ,且
,且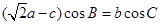 .
.(1)求角
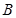 的大小;
的大小;(2)设向量
 ,且
,且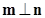 ,求
,求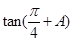 的值.
的值.(1) ;(2)
;(2)  .
.
 ;(2)
;(2)  .
.试题分析:(1)
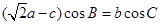 这个等式中既有边又有角,这种等式一般有两种考虑:要么只留边,要么只留角.在本题中这两种方法都行.
这个等式中既有边又有角,这种等式一般有两种考虑:要么只留边,要么只留角.在本题中这两种方法都行.思路一、由正弦定理得:
 ,然后用三角函数公式可求出
,然后用三角函数公式可求出 .
.思路二、由余弦定理得:
 ,化简得
,化简得 .再由余弦定理可得
.再由余弦定理可得 .
.(2)由
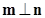 得;
得; 解这个方程,可求出
解这个方程,可求出 的值,再用正切和角公式可求出
的值,再用正切和角公式可求出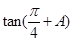 .
.试题解析:(1)法一、






 6分
6分法二、由余弦定理得:
 ,化简得:
,化简得: ,
,即
 .
.所以
 ,
, 6分
6分(2)


 或者
或者 .
.当
 时,
时, (舍去);
(舍去);当
 时,
时, . 12分
. 12分
练习册系列答案
相关题目
 acos C.
acos C.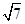 ,且
,且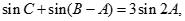 求△ABC的面积.
求△ABC的面积. 中,
中, 分别是
分别是 的对边长,已知
的对边长,已知 ,求
,求 的大小及
的大小及 的值.
的值. 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,设S为△ABC的面积,满足
,设S为△ABC的面积,满足 .
. ,且
,且 ,求
,求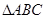 中,内角
中,内角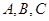 的对边分别为
的对边分别为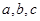 . 已知
. 已知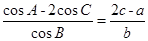 .
.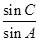 的值; (2) 若
的值; (2) 若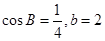 ,求
,求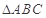 中,已知角
中,已知角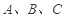 的对边分别为
的对边分别为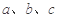 .向量
.向量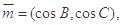
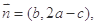 且向量
且向量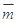 与
与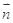 共线.
共线.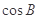 的值;
的值;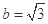 ,求
,求 中
中 分别为内角
分别为内角 的对边,已知
的对边,已知 则
则 ______.
______. 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 ,则边长
,则边长 .
. 中,若
中,若 ,
, ,
, ,则
,则 的大小为_________.
的大小为_________.