题目内容
已知直线l:y=x+m,m∈R.
(1)若以点M(2,0)为圆心的圆与直线l相切于点P,且点P在y轴上,求该圆的方程.
(2)若直线l关于x轴对称的直线为l′,问直线l′与抛物线C:x2=4y是否相切?说明理由.
设所求圆的半径为r,则圆的方程可设为(x-2)2+y2=r2.
依题意,所求圆与直线l:x-y+m=0相切于点P(0,m),
则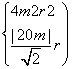 解得
解得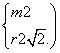
所以所求圆的方程为(x-2)2+y2=8. --------------6 分
(2)因为直线l的方程为y=x+m,
所以直线l′的方程为y=-x-m. --------------7分
由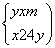 得x2+4x+4m=0. ------------
得x2+4x+4m=0. ------------ -8分
-8分
Δ=42-4×4m=16(1-m).--------------9分
①当m=1,即Δ=0时,直线l′与抛物线C相切;
②当m≠1,即Δ≠0时,直线l′与抛物线C不相切.
综上,当m=1时,直线l′与抛物线C相切;当m≠1时,直线l′与抛物线C不相切------12分 

练习册系列答案
相关题目
 ,
, ,函数
,函数 ,
, 三个内角
三个内角 的对边分别为
的对边分别为 .
. 的单调递增区间;
的单调递增区间;
 ,求
,求 的面积
的面积 .
. 的导函数在区间
的导函数在区间 上的图像关于直线
上的图像关于直线 对称,则函数
对称,则函数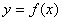 在区间
在区间 上的图象可能是
上的图象可能是
 B.
B. C.
C. D.
D.
 满足
满足 ,则
,则 _________.
_________.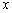 轴的正半轴重合.设点
轴的正半轴重合.设点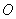 为坐标原点, 直线
为坐标原点, 直线
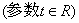 与曲线C的极坐标方程为
与曲线C的极坐标方程为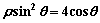 .
.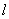 与曲线
与曲线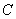 的普通方程;
的普通方程;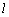 与曲线
与曲线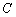 相交于A,B两点,求证:
相交于A,B两点,求证: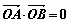 .
. ,
, ”的否定是 .
”的否定是 . 对任意
对任意 恒成立,则实数
恒成立,则实数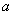 的取值范围为
的取值范围为 B.
B. C.
C. D.
D. 