题目内容
9.求下列各式的值:(1)${(2\frac{1}{4})^{\frac{1}{2}}}$-${(π-1)^0}-{(3\frac{3}{8})^{-\frac{2}{3}}}$; (2)${log_3}^{\frac{{\sqrt{3}}}{3}}$+lg5+lg0.2+${7^{{{log}_7}^2}}$.
分析 (1)化带分数为假分数,化负指数为正指数,然后利用有理指数幂的运算性质化简求值;
(2)化根式为分数指数幂,然后利用对数的运算性质化简求值.
解答 解:(1)${(2\frac{1}{4})^{\frac{1}{2}}}$-${(π-1)^0}-{(3\frac{3}{8})^{-\frac{2}{3}}}$=$[(\frac{3}{2})^{2}]^{\frac{1}{2}}-1-[(\frac{3}{2})^{3}]^{-\frac{2}{3}}$=$\frac{3}{2}-1-\frac{4}{9}$=$\frac{1}{18}$;
(2)${log_3}^{\frac{{\sqrt{3}}}{3}}$+lg5+lg0.2+${7^{{{log}_7}^2}}$=$lo{g}_{3}{3}^{-\frac{1}{2}}+lg(5×0.2)+2=-\frac{1}{2}+2=\frac{3}{2}$.
点评 本题考查有理指数幂的化简求值,考查对数的运算性质,是基础的计算题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
14.记函数f(x)($\frac{1}{e}$<x≤e,e=2.71828…是自然对数的底数)的导数为f′(x),函数g(x)=(x-$\frac{1}{\sqrt{e}}$)f′(x)只有一个零点,且g(x)的图象不经过第一象限,当x>$\frac{1}{e}$时,f(x)+4lnx+$\frac{1}{lnx+1}$>$\frac{1}{\sqrt{e}}$,f[f(x)+4lnx+$\frac{1}{lnx+1}$]=0,下列关于f(x)的结论,成立的是( )
| A. | 当x=e时,f(x)取得最小值 | B. | f(x)最大值为1 | ||
| C. | 不等式f(x)<0的解集是(1,e) | D. | 当$\frac{1}{e}$<x<1时,f(x)>0 |
18.对任意的实数x,若[x]表示不超过x的最大整数,则“-1<x-y<1”是“[x]=[y]”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
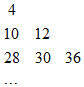 设数列{an}是集合{x|x=3s+3t,s<t且s,t∈N}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图的等腰直角三角形数表,则a15的值为324.
设数列{an}是集合{x|x=3s+3t,s<t且s,t∈N}中所有的数从小到大排列成的数列,即a1=4,a2=10,a3=12,a4=28,a5=30,a6=36,…,将数列{an}中各项按照上小下大,左小右大的原则排成如图的等腰直角三角形数表,则a15的值为324.