题目内容
9.已知x,y满足$\left\{\begin{array}{l}{2x-y+1≤0}\\{2x+y+5≥0}\\{x-y+1≥0}\end{array}\right.$,则z=$\frac{x+1}{x+2y-3}$的取值范围是[-1,$\frac{1}{7}$].分析 由题意作平面区域,分类讨论当x≠-1时,化简z=$\frac{x+1}{x+2y-3}$=$\frac{1}{1+2\frac{y-2}{x+1}}$,从而利用几何意义求解.
解答 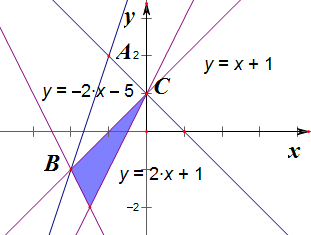 解:由题意作平面区域如下,
解:由题意作平面区域如下,
当x=-1时,z=$\frac{x+1}{x+2y-3}$=0;
当x≠-1时,z=$\frac{x+1}{x+2y-3}$=$\frac{1}{1+2\frac{y-2}{x+1}}$,
易知A(-1,2),B(-2,-1),C(0,1);
故kAB=$\frac{2+1}{-1+2}$=3,kAC=$\frac{2-1}{-1-0}$=-1,
故$\frac{y-2}{x+1}$≥3或$\frac{y-2}{x+1}$≤-1,
故1+2$\frac{y-2}{x+1}$≥7或1+2$\frac{y-2}{x+1}$≤-1;
故0<$\frac{1}{1+2\frac{y-2}{x+1}}$≤$\frac{1}{7}$或-1≤$\frac{1}{1+2\frac{y-2}{x+1}}$<0;
综上所述,-1≤$\frac{1}{1+2\frac{y-2}{x+1}}$≤$\frac{1}{7}$.
故答案为:[-1,$\frac{1}{7}$].
点评 本题考查了线性规划,同时考查了数形结合的思想方法应用及分类讨论的思想应用.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
4.在[0,π]内任意取一个数x,使得sinx+$\sqrt{3}$cosx≥1的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
14.已知定义在R上的奇函数满足f(x+1)=-f(x),且在[0,1)上单调递增,记a=f($\frac{1}{2}$),b=f(2),c=f(3),则a,b,c的大小关系为( )
| A. | a>b=c | B. | b>a=c | C. | b>c>a | D. | a>c>b |
1.在直角三角形ABC中,直角顶点为C,其中∠B=60°,在角ACB内部任作一条射线CM,与线段AB交于点M,满足AM<AC的概率为$\frac{5}{6}$,则满足BC<AM<AC的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |