题目内容
下列物体的三视图与物体摆放位置无关的是（ ）
| A．正方体 | B．正四面体 | C．正三棱锥 | D．球 |
D
解析试题分析：球的正视图，侧视图，俯视图都是过球心的大圆，三视图相同。正方体，正四面体，正三棱锥的三视图与几何体摆放的角度有关，当角度不同时，三视图不同
考点：三视图
点评：本题要求掌握常见几何体：棱柱棱锥圆柱圆锥及球的三视图的特点及画法
练习册系列答案
相关题目
已知圆柱
底面半径为1，高为
，
是圆柱的一个轴截面．动点
从点
出发沿着圆柱的侧面到达点
，其距离最短时在侧面留下的曲线
如图所示．
现将轴截面绕着轴逆时针旋转
后，边
与曲线相交于点
，设
的长度为
，则
的图象大致为（ ）
某个几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的表面积是（ ）
A． | B． |
C．6+ | D． |
一个三棱锥的三视图如图所示，则该几何体的表面积为（ ）
A． | B． |
C． | D．8 |
一个棱锥的三视图如图，则该棱锥的表面积（单位：c
）为（ ）
A．48+12 | B．48+24 | C．36+12 | D．36+24 |
若某空间几何体的三视图如图所示，则该几何体的体积是（ ）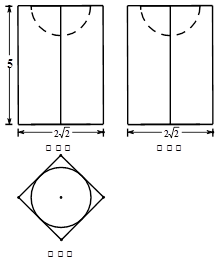
| A．20-2π | B． | C． | D． |
某几何体的三视图如图所示，则其侧面积为( )
A． | B． | C． | D． |
图中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得．现用一个竖直的平面去截这个几何体，则截面图形可能是 ( )
| A．(1)(2) | B．(1)(3) | C．(1)(4) | D．(1)(5) |
某空间几何体的三视图及尺寸如图1，则该几何体的体积是
A． | B． | C． | D． |