题目内容
4.设$\overrightarrow a•\overrightarrow b=4\sqrt{3}$,若$\overrightarrow a$在$\overrightarrow b$方向上投影为$2\sqrt{3}$,$\overrightarrow b$在$\overrightarrow a$方向上的投影为$\sqrt{3}$,则$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{6}$.分析 运用向量的投影定义,可得|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,再由cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$,计算即可得到所求夹角.
解答 解:$\overrightarrow a•\overrightarrow b=4\sqrt{3}$,
若$\overrightarrow a$在$\overrightarrow b$方向上投影为$2\sqrt{3}$,$\overrightarrow b$在$\overrightarrow a$方向上的投影为$\sqrt{3}$,
可得$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=2$\sqrt{3}$,$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=$\sqrt{3}$,
即有|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=2,
则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{4\sqrt{3}}{4×2}$=$\frac{\sqrt{3}}{2}$,
由0≤<$\overrightarrow{a}$,$\overrightarrow{b}$>≤π,
可得$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{6}$.
故答案为:$\frac{π}{6}$.
点评 本题考查向量的夹角的求法,注意运用向量的投影概念和向量数量积的夹角公式,考查运算能力,属于基础题.

 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | 25 | B. | 24 | C. | 21 | D. | 30 |
| A. | 1 | B. | 2 | C. | $\frac{4}{5}$ | D. | $\frac{2}{5}$ |
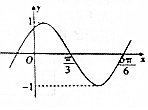 已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.
已知函数y=sin(ωx+φ)(ω>0,0<φ≤$\frac{π}{2}$)的部分图象如图所示,则cos(5ωφ)=-$\frac{1}{2}$.